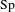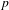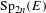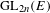2 results
ON
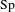 $\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
$\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 17 April 2019, pp. 225-276
- Print publication:
- January 2021
-
- Article
- Export citation
Tame Supercuspidal Representations of GL(n) Distinguished by a Unitary Group
-
- Journal:
- Compositio Mathematica / Volume 133 / Issue 2 / September 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 199-244
- Print publication:
- September 2002
-
- Article
-
- You have access
- Export citation