One of the elegant achievements in the history of proof theory is the characterization of the provably total recursive functions of an arithmetical theory by its proof-theoretic ordinal as a way to measure the time complexity of the functions. Unfortunately, the machinery is not sufficiently fine-grained to be applicable on the weak theories, on the one hand and to capture the bounded functions with bounded definitions of strong theories, on the other. In this paper, we develop such a machinery to address the bounded theorems of both strong and weak theories of arithmetic. In the first part, we provide a refined version of ordinal analysis to capture the feasibly definable and bounded functions that are provably total in 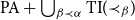$\textrm{PA}+\bigcup _{\beta \prec \alpha } \textrm{TI}({\prec_{\beta}})$, the extension of Peano arithmetic by transfinite induction up to the ordinals below 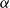$\alpha$. Roughly speaking, we identify the functions as the ones that are computable by a sequence of 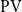$\textrm{PV}$-provable polynomial time modifications on an initial polynomial time value, where the computational steps are indexed by the ordinals below 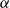$\alpha$, decreasing by the modifications. In the second part, and choosing 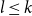$l \leq k$, we use similar technique to capture the functions with bounded definitions in the theory 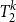$T^k_2$ (resp. 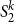$S^k_2$) as the functions computable by exponentially (resp. polynomially) long sequence of 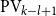$\textrm{PV}_{k-l +1}$-provable reductions between 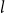$l$-turn games starting with an explicit 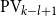$\textrm{PV}_{k-l +1}$-provable winning strategy for the first game.

We introduce and analyze a new axiomatic theory $\mathsf {CD}$ of truth. The primitive truth predicate can be applied to sentences containing the truth predicate. The theory is thoroughly classical in the sense that $\mathsf {CD}$ is not only formulated in classical logic, but that the axiomatized notion of truth itself is classical: The truth predicate commutes with all quantifiers and connectives, and thus the theory proves that there are no truth value gaps or gluts. To avoid inconsistency, the instances of the T-schema are restricted to determinate sentences. Determinateness is introduced as a further primitive predicate and axiomatized. The semantics and proof theory of $\mathsf {CD}$ are analyzed.

We present an analogue of Gödel’s second incompleteness theorem for systems of second-order arithmetic. Whereas Gödel showed that sufficiently strong theories that are $\Pi ^0_1$-sound and $\Sigma ^0_1$-definable do not prove their own $\Pi ^0_1$-soundness, we prove that sufficiently strong theories that are $\Pi ^1_1$-sound and $\Sigma ^1_1$-definable do not prove their own $\Pi ^1_1$-soundness. Our proof does not involve the construction of a self-referential sentence but rather relies on ordinal analysis.

By Solovay’s celebrated completeness result [31] on formal provability we know that the provability logic ${\textbf {GL}}$ describes exactly all provable structural properties for any sound and strong enough arithmetical theory with a decidable axiomatisation. Japaridze generalised this result in [22] by considering a polymodal version ${\mathsf {GLP}}$ of ${\textbf {GL}}$ with modalities $[n]$ for each natural number n referring to ever increasing notions of provability. Modern treatments of ${\mathsf {GLP}}$ tend to interpret the $[n]$ provability notion as “provable in a base theory T together with all true $\Pi ^0_n$ formulas as oracles.” In this paper we generalise this interpretation into the transfinite. In order to do so, a main difficulty to overcome is to generalise the syntactical characterisations of the oracle formulas of complexity $\Pi ^0_n$ to the hyper-arithmetical hierarchy. The paper exploits the fact that provability is $\Sigma ^0_1$ complete and that similar results hold for stronger provability notions. As such, the oracle sentences to define provability at level $\alpha $ will recursively be taken to be consistency statements at lower levels: provability through provability whence the name of the paper. The paper proves soundness and completeness for the proposed interpretation for a wide class of theories, namely for any theory that can formalise the recursion described above and that has some further very natural properties. Some remarks are provided on how the recursion can be formalised into second order arithmetic and on lowering the proof-theoretical strength of these systems of second order arithmetic.

Questions concerning the proof-theoretic strength of classical versus nonclassical theories of truth have received some attention recently. A particularly convenient case study concerns classical and nonclassical axiomatizations of fixed-point semantics. It is known that nonclassical axiomatizations in four- or three-valued logics are substantially weaker than their classical counterparts. In this paper we consider the addition of a suitable conditional to First-Degree Entailment—a logic recently studied by Hannes Leitgeb under the label HYPE. We show in particular that, by formulating the theory PKF over HYPE, one obtains a theory that is sound with respect to fixed-point models, while being proof-theoretically on a par with its classical counterpart KF. Moreover, we establish that also its schematic extension—in the sense of Feferman—is as strong as the schematic extension of KF, thus matching the strength of predicative analysis.

It is well-known that natural axiomatic theories are well-ordered by consistency strength. However, it is possible to construct descending chains of artificial theories with respect to consistency strength. We provide an explanation of this well-orderedness phenomenon by studying a coarsening of the consistency strength order, namely, the $\Pi ^1_1$ reflection strength order. We prove that there are no descending sequences of $\Pi ^1_1$ sound extensions of $\mathsf {ACA}_0$ in this ordering. Accordingly, we can attach a rank in this order, which we call reflection rank, to any $\Pi ^1_1$ sound extension of $\mathsf {ACA}_0$ . We prove that for any $\Pi ^1_1$ sound theory T extending $\mathsf {ACA}_0^+$ , the reflection rank of T equals the $\Pi ^1_1$ proof-theoretic ordinal of T. We also prove that the $\Pi ^1_1$ proof-theoretic ordinal of $\alpha $ iterated $\Pi ^1_1$ reflection is $\varepsilon _\alpha $ . Finally, we use our results to provide straightforward well-foundedness proofs of ordinal notation systems based on reflection principles.

In this paper we introduce a notation system for the infinitary derivations occurring in the ordinal analysis of KP + Π3-Reflection due to Michael Rathjen. This allows a finitary ordinal analysis of KP + Π3-Reflection. The method used is an extension of techniques developed by Wilfried Buchholz, namely operator controlled notation systems for RS∞-derivations. Similarly to Buchholz we obtain a characterisation of the provably recursive functions of KP + Π3-Reflection as <-recursive functions where < is the ordering on Rathjen's ordinal notation system . 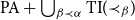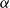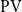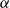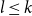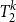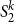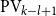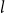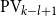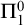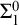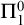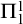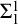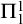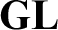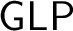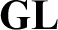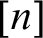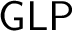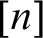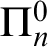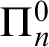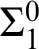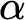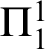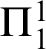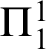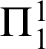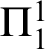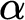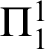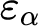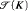Further we show a conservation result for 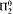-sentences.