An extension of a result of Sela shows that if Γ is a torsion-free word hyperbolic group, then the only homomorphisms Γ→Γ with finite-index image are the automorphisms. It follows from this result and properties of quasiregular mappings, that if M is a closed Riemannian n-manifold with negative sectional curvature (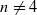 ), then every quasiregular mapping f:M→M is a homeomorphism. In the constant-curvature case the dimension restriction is not necessary and Mostow rigidity implies that f is homotopic to an isometry. This is to be contrasted with the fact that every such manifold admits a non-homeomorphic light open self-mapping. We present similar results for more general quotients of hyperbolic space and quasiregular mappings between them. For instance, we establish that besides covering projections there are no π1-injective proper quasiregular mappings f:M→N between hyperbolic 3-manifolds M and N with non-elementary fundamental group.
), then every quasiregular mapping f:M→M is a homeomorphism. In the constant-curvature case the dimension restriction is not necessary and Mostow rigidity implies that f is homotopic to an isometry. This is to be contrasted with the fact that every such manifold admits a non-homeomorphic light open self-mapping. We present similar results for more general quotients of hyperbolic space and quasiregular mappings between them. For instance, we establish that besides covering projections there are no π1-injective proper quasiregular mappings f:M→N between hyperbolic 3-manifolds M and N with non-elementary fundamental group.

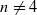 ), then every quasiregular mapping
), then every quasiregular mapping 