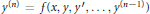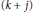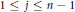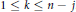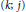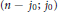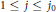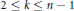1 results
Uniqueness Implies Existence and Uniqueness Conditions for a Class of (k + j)-Point Boundary Value Problems for n-th Order Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-296
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
-
For the
$n$-th order nonlinear differential equation,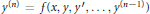 
${{y}^{(n)}}\,=\,f(x,\,y,\,y\prime ,\ldots ,\,{{y}^{(n-1)}})$, we consider uniqueness implies uniqueness and existence results for solutions satisfying certain 
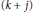$(k\,+\,j)$-point boundary conditions for 
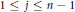$1\,\le \,j\,\le \,n\,-\,1$ and 
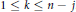$1\,\le \,k\,\le \,n\,-\,j$. We define 
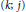$(k;\,j)$-point unique solvability in analogy to 
$k$-point disconjugacy and we show that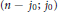 
$(n\,-\,{{j}_{0}};\,{{j}_{0}})$-point unique solvability implies 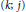$(k;\,j)$-point unique solvability for 
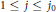$1\,\le \,j\,\le \,{{j}_{0}}$, and 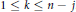$1\,\le \,k\,\le \,n\,-\,j$. This result is analogous to $n$-point disconjugacy implies $k$-point disconjugacy for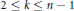 
$2\,\le \,k\,\le \,n\,-\,1$.
