1 results
Multiplicity and stability of normalized solutions to non-autonomous Schrödinger equation with mixed non-linearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
-
This paper first studies the multiplicity of normalized solutions to the non-autonomous Schrödinger equation with mixed nonlinearities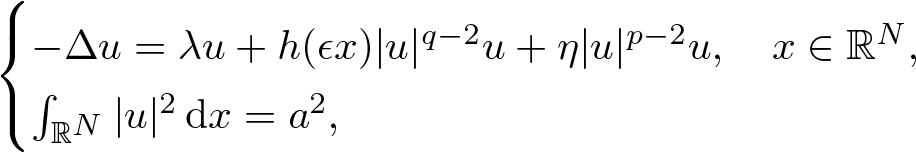
where
\begin{equation*}\begin{cases}-\Delta u=\lambda u+h(\epsilon x)|u|^{q-2}u+\eta |u|^{p-2}u,\quad x\in \mathbb{R}^N, \\\int_{\mathbb{R}^N}|u|^2\,\textrm{d}x=a^2,\end{cases}\end{equation*}
$a, \epsilon, \eta \gt 0$, q is L2-subcritical, p is L2-supercritical,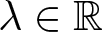 
$\lambda\in \mathbb{R}$ is an unknown parameter that appears as a Lagrange multiplier and h is a positive and continuous function. It is proved that the numbers of normalized solutions are at least the numbers of global maximum points of h when ϵ is small enough. The solutions obtained are local minimizers and probably not ground state solutions for the lack of symmetry of the potential h. Secondly, the stability of several different sets consisting of the local minimizers is analysed. Compared with the results of the corresponding autonomous equation, the appearance of the potential h increases the number of the local minimizers and the number of the stable sets. In particular, our results cover the Sobolev critical case 
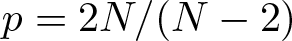$p=2N/(N-2)$.
