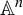2 results
Dynamical degrees of affine-triangular automorphisms of affine spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 3551-3592
- Print publication:
- December 2022
-
- Article
- Export citation
Semistable reduction for overconvergent F-isocrystals, III: Local semistable reduction at monomial valuations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 143-172
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation