For a smooth projective surface 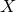 $X$ satisfying
$X$ satisfying 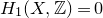 $H_1(X,\mathbb{Z}) = 0$ and
$H_1(X,\mathbb{Z}) = 0$ and 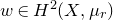 $w \in H^2(X,\mu _r)$, we study deformation invariants of the pair
$w \in H^2(X,\mu _r)$, we study deformation invariants of the pair 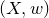 $(X,w)$. Choosing a Brauer–Severi variety
$(X,w)$. Choosing a Brauer–Severi variety 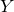 $Y$ (or, equivalently, Azumaya algebra
$Y$ (or, equivalently, Azumaya algebra 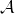 $\mathcal{A}$) over
$\mathcal{A}$) over 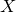 $X$ with Stiefel–Whitney class
$X$ with Stiefel–Whitney class 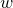 $w$, the invariants are defined as virtual intersection numbers on suitable moduli spaces of stable twisted sheaves on
$w$, the invariants are defined as virtual intersection numbers on suitable moduli spaces of stable twisted sheaves on 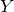 $Y$ constructed by Yoshioka (or, equivalently, moduli spaces of
$Y$ constructed by Yoshioka (or, equivalently, moduli spaces of 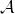 $\mathcal{A}$-modules of Hoffmann–Stuhler).
$\mathcal{A}$-modules of Hoffmann–Stuhler).
We show that the invariants do not depend on the choice of 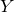 $Y$. Using a result of de Jong, we observe that they are deformation invariants of the pair
$Y$. Using a result of de Jong, we observe that they are deformation invariants of the pair 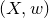 $(X,w)$. For surfaces with
$(X,w)$. For surfaces with 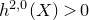 $h^{2,0}(X) \gt 0$, we show that the invariants can often be expressed as virtual intersection numbers on Gieseker–Maruyama–Simpson moduli spaces of stable sheaves on
$h^{2,0}(X) \gt 0$, we show that the invariants can often be expressed as virtual intersection numbers on Gieseker–Maruyama–Simpson moduli spaces of stable sheaves on 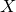 $X$. This can be seen as a
$X$. This can be seen as a 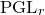 ${\rm PGL}_r$–
${\rm PGL}_r$–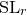 ${\rm SL}_r$ correspondence.
${\rm SL}_r$ correspondence.
As an application, we express 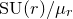 ${\rm SU}(r) / \mu _r$ Vafa–Witten invariants of
${\rm SU}(r) / \mu _r$ Vafa–Witten invariants of 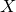 $X$ in terms of
$X$ in terms of 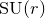 ${\rm SU}(r)$ Vafa–Witten invariants of
${\rm SU}(r)$ Vafa–Witten invariants of 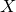 $X$. We also show how formulae from Donaldson theory can be used to obtain upper bounds for the minimal second Chern class of Azumaya algebras on
$X$. We also show how formulae from Donaldson theory can be used to obtain upper bounds for the minimal second Chern class of Azumaya algebras on 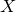 $X$ with given division algebra at the generic point.
$X$ with given division algebra at the generic point.
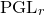 ${\rm PGL}_r$–
${\rm PGL}_r$–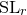 ${\rm SL}_r$ correspondence for projective surfaces
${\rm SL}_r$ correspondence for projective surfaces