1 results
Perverse, Hodge and motivic realizations of étale motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 1237-1285
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
-
Let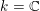
$k=\mathbb{C}$ be the field of complex numbers. In this article we construct Hodge realization functors defined on the triangulated categories of étale motives with rational coefficients. Our construction extends to every smooth quasi-projective 
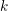$k$-scheme, the construction done by Nori over a field, and relies on the original version of the basic lemma proved by Beĭlinson. As in the case considered by Nori, the realization functor factors through the bounded derived category of a perverse version of the Abelian category of Nori motives.
