We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It has been shown that the Mere Addition Paradox occurs in a choice-functional approach with Path Independence (Stewart R.T., 2021, Path independence and a persistent paradox of population ethics, Journal of Philosophy, forthcoming). The present study is a three-part response to this finding. First, I show that Path Independence is not an essential property leading to this paradox and that logically weaker properties can get the same result. Second, I present a rationalizable choice function that does not yield the paradox. And third, I argue that menu-dependent relations are nicely examined if Path Independence is relaxed to Property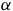 
$\alpha $ (or equivalently, Contraction Consistency).
