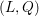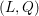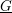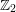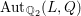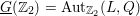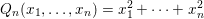3 results
Where are the zeroes of a random p-adic polynomial?
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Group schemes and local densities of quadratic lattices in residue characteristic 2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 793-827
- Print publication:
- May 2015
-
- Article
- Export citation
On the mass formula of supersingular abelian varieties with real multiplications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 373-392
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation