We prove the existence of solitary wave solutions to the quasilinear Benney system
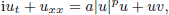
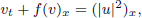
where 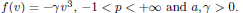 , –1 < p < +∞ and a, γ > 0. We establish, in particular, the existence of travelling waves with speed arbitrarily large if p < 0 and arbitrarily close to 0 if
, –1 < p < +∞ and a, γ > 0. We establish, in particular, the existence of travelling waves with speed arbitrarily large if p < 0 and arbitrarily close to 0 if 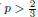 . We also show the existence of standing waves in the case
. We also show the existence of standing waves in the case 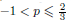 , with compact support if – 1 < p < 0. Finally, we obtain, under certain conditions, the linearized stability of such solutions.
, with compact support if – 1 < p < 0. Finally, we obtain, under certain conditions, the linearized stability of such solutions.