1 results
On accurately estimating stability thresholds for periodic spot patterns of reaction-diffusion systems in
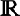 $\mathbb{R}$2
$\mathbb{R}$2
-
- Journal:
- European Journal of Applied Mathematics / Volume 26 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 04 March 2015, pp. 325-353
-
- Article
- Export citation