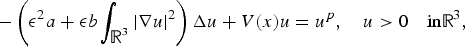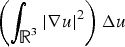1 results
Multi-peak positive solutions to a class of Kirchhoff equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1097-1122
- Print publication:
- August 2019
-
- Article
- Export citation
-
In the present paper, we consider the nonlocal Kirchhoff problem
where a, b>0, 1<p<5 are constants, ϵ>0 is a parameter. Under some mild assumptions on the function V, we obtain multi-peak solutions for ϵ sufficiently small by Lyapunov–Schmidt reduction method. Even though many results on single peak solutions to singularly perturbed Kirchhoff problems have been derived in the literature by various methods, there exist no results on multi-peak solutions before this paper, due to some difficulties caused by the nonlocal term
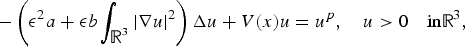$$-\left(\epsilon^2a+\epsilon b\int_{{\open R}^{3}}\vert \nabla u \vert^{2}\right)\Delta u+V(x)u=u^{p}, \quad u \gt 0 \quad {\rm in} {\open R}^{3},$$
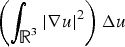$\left(\int_{{\open R}^{3}} \vert \nabla u \vert^{2}\right)\Delta u$. A remarkable new feature of this problem is that the corresponding unperturbed problem turns out to be a system of partial differential equations, but not a single Kirchhoff equation, which is quite different from most of the elliptic singular perturbation problems.
