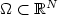We consider a nonlinear second order elliptic boundary value problem (BVP)in a bounded domain $\Omega\subset {\mathbb R}^N$ 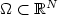 witha nonlocal boundary condition. A Dirichlet BC containing an unknown additive constant,accompanied with a nonlocal (integral) Neumann side condition is prescribed at some boundary part Γn . The rest of the boundary is equipped with Dirichlet or nonlinear Robin type BC. The solution is found via linearization. We design a robust and efficient approximation scheme. Error estimates for the linearization algorithm are derived inL 2(Ω),H 1(Ω) andL ∞(Ω) spaces.
witha nonlocal boundary condition. A Dirichlet BC containing an unknown additive constant,accompanied with a nonlocal (integral) Neumann side condition is prescribed at some boundary part Γn . The rest of the boundary is equipped with Dirichlet or nonlinear Robin type BC. The solution is found via linearization. We design a robust and efficient approximation scheme. Error estimates for the linearization algorithm are derived inL 2(Ω),H 1(Ω) andL ∞(Ω) spaces.