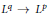6 results
The Advantages of an Attenuated Total Internal Reflection Infrared Microspectroscopic Imaging Technique for the Analysis of Polymer Laminates
-
- Journal:
- / Volume 21 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 18 May 2015, pp. 626-636
- Print publication:
- June 2015
-
- Article
- Export citation
Stability for Leipholz’s Type of Laminated Box Columns with Nonsymmetric Lay-Ups on Elastic Foundation
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 March 2015, pp. 158-179
- Print publication:
- April 2015
-
- Article
- Export citation
Sharp Localized Inequalities for Fourier Multipliers
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1358-1381
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Which electric fields are realizable in conducting materials?
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 20 January 2014, pp. 307-323
- Print publication:
- March 2014
-
- Article
- Export citation
Prediction of delamination crack growth in carbon/fiber epoxy composite laminates using non-local interface damage model
-
- Journal:
- Mechanics & Industry / Volume 15 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 293-300
- Print publication:
- 2014
-
- Article
- Export citation
Mechanical Properties of a Centrally Notched APC-2 Composite Laminate Due to Fatigue Loading at Elevated Temperature (II)
-
- Journal:
- Journal of Mechanics / Volume 25 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 05 May 2011, pp. 251-259
- Print publication:
- September 2009
-
- Article
- Export citation