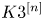 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
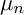 $\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
$\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
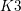 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
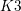 $K3$ surfaces
$K3$ surfaces
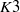 $K 3$ surfaces
$K 3$ surfaces