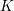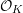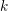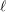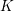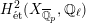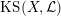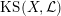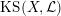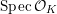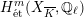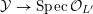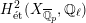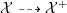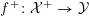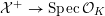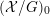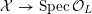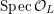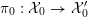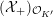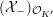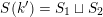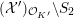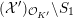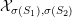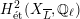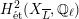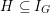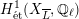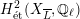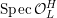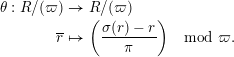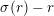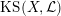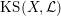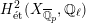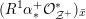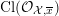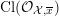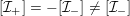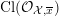1 Introduction
Let
![]() ${\mathcal{O}}_{K}$
be a local Henselian DVR (discrete valuation ring) of characteristic zero with field of fractions
${\mathcal{O}}_{K}$
be a local Henselian DVR (discrete valuation ring) of characteristic zero with field of fractions
![]() $K$
and perfect residue field
$K$
and perfect residue field
![]() $k$
, whose characteristic is
$k$
, whose characteristic is
![]() $p\geqslant 0$
. For example,
$p\geqslant 0$
. For example,
![]() ${\mathcal{O}}_{K}$
could be
${\mathcal{O}}_{K}$
could be
![]() $\mathbb{C}[[t]]$
or the ring of integers in a
$\mathbb{C}[[t]]$
or the ring of integers in a
![]() $p$
-adic field. Given a variety
$p$
-adic field. Given a variety
![]() $X$
that is smooth and proper over
$X$
that is smooth and proper over
![]() $K$
, one can ask whether
$K$
, one can ask whether
![]() $X$
has good reduction, that is, whether there exists an algebraic space
$X$
has good reduction, that is, whether there exists an algebraic space
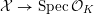 $$\begin{eqnarray}{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}\end{eqnarray}$$
with generic fiber
![]() $X$
that is smooth and proper over
$X$
that is smooth and proper over
![]() ${\mathcal{O}}_{K}$
.
${\mathcal{O}}_{K}$
.
1.1 Good reduction and Galois representations
Let
![]() $\ell$
be a prime different from
$\ell$
be a prime different from
![]() $p$
, let
$p$
, let
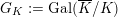 $G_{K}:=\operatorname{Gal}(\overline{K}/K)$
be the absolute Galois group of
$G_{K}:=\operatorname{Gal}(\overline{K}/K)$
be the absolute Galois group of
![]() $K$
, and let
$K$
, and let
![]() $I_{K}$
be its inertia subgroup. Then the natural
$I_{K}$
be its inertia subgroup. Then the natural
![]() $\ell$
-adic Galois representation
$\ell$
-adic Galois representation
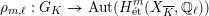 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{m,\ell }:G_{K}\rightarrow \operatorname{Aut}(H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{m,\ell }:G_{K}\rightarrow \operatorname{Aut}(H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
is called unramified if it satisfies
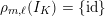 $\unicode[STIX]{x1D70C}_{m,\ell }(I_{K})=\{\operatorname{id}\}$
. A necessary condition for
$\unicode[STIX]{x1D70C}_{m,\ell }(I_{K})=\{\operatorname{id}\}$
. A necessary condition for
![]() $X$
to have good reduction is that for all
$X$
to have good reduction is that for all
![]() $m\geqslant 1$
and all primes
$m\geqslant 1$
and all primes
![]() $\ell \neq p$
, the representation
$\ell \neq p$
, the representation
![]() $\unicode[STIX]{x1D70C}_{m,\ell }$
is unramified.
$\unicode[STIX]{x1D70C}_{m,\ell }$
is unramified.
1.2 Curves and Abelian varieties
By a famous theorem of Serre and Tate [Reference Serre and TateST68], which generalizes results of Néron, Ogg, and Shafarevich for elliptic curves to Abelian varieties, the
![]() $G_{K}$
-representation
$G_{K}$
-representation
![]() $\unicode[STIX]{x1D70C}_{1,\ell }$
detects the reduction type of Abelian varieties.
$\unicode[STIX]{x1D70C}_{1,\ell }$
detects the reduction type of Abelian varieties.
Theorem 1.1 (Serre–Tate).
An Abelian variety
![]() $X$
over
$X$
over
![]() $K$
has good reduction if and only if the
$K$
has good reduction if and only if the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
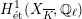 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.
On the other hand, it is not too difficult to give counterexamples to such a result for curves of genus at least
![]() $2$
. Nevertheless, Oda [Reference OdaOda95] showed that good reduction can be detected by the outer
$2$
. Nevertheless, Oda [Reference OdaOda95] showed that good reduction can be detected by the outer
![]() $G_{K}$
-representation on the étale fundamental group. We refer the interested reader to § 2.4 for references, examples, and details.
$G_{K}$
-representation on the étale fundamental group. We refer the interested reader to § 2.4 for references, examples, and details.
1.3 Kulikov–Nakkajima–Persson–Pinkham models
Before coming to the results of this article, we have to make one crucial assumption.
Assumption
 $(\star )$
.
$(\star )$
.
A K3 surface
![]() $X$
over
$X$
over
![]() $K$
satisfies Assumption (
$K$
satisfies Assumption (
![]() $\star$
) if there exists a finite field extension
$\star$
) if there exists a finite field extension
![]() $L/K$
such that
$L/K$
such that
![]() $X_{L}$
admits a model
$X_{L}$
admits a model
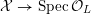 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
that is a regular algebraic space with trivial canonical sheaf
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
that is a regular algebraic space with trivial canonical sheaf
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
, and whose geometric special fiber is a normal crossing divisor.
$\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
, and whose geometric special fiber is a normal crossing divisor.
In equal characteristic zero, Assumption (
![]() $\star$
) always holds, and the special fibers of the corresponding models have been classified by Kulikov [Reference KulikovKul77], Persson [Reference PerssonPer77], and Persson and Pinkham [Reference Persson and PinkhamPP81]. In mixed characteristic, the corresponding classification (assuming the existence of such models) is due to Nakkajima [Reference NakkajimaNakk00]. If the expected results on resolution of singularities and toroidalization of morphisms were known to hold in mixed characteristic, then Assumption
$\star$
) always holds, and the special fibers of the corresponding models have been classified by Kulikov [Reference KulikovKul77], Persson [Reference PerssonPer77], and Persson and Pinkham [Reference Persson and PinkhamPP81]. In mixed characteristic, the corresponding classification (assuming the existence of such models) is due to Nakkajima [Reference NakkajimaNakk00]. If the expected results on resolution of singularities and toroidalization of morphisms were known to hold in mixed characteristic, then Assumption
![]() $(\star )$
would follow from Kawamata’s semi-stable minimal model program (MMP) in mixed characteristic [Reference KawamataKaw94] and Artin’s results [Reference ArtinArt74] on simultaneous resolutions of families of surface singularities. We refer to Proposition 3.1 for details. Using work of Maulik [Reference MaulikMau14] and some strengthenings due to the second named author [Reference MatsumotoMat15], we have at least the following.
$(\star )$
would follow from Kawamata’s semi-stable minimal model program (MMP) in mixed characteristic [Reference KawamataKaw94] and Artin’s results [Reference ArtinArt74] on simultaneous resolutions of families of surface singularities. We refer to Proposition 3.1 for details. Using work of Maulik [Reference MaulikMau14] and some strengthenings due to the second named author [Reference MatsumotoMat15], we have at least the following.
Theorem 1.2. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
and assume that
$K$
and assume that
![]() $p=0$
or that
$p=0$
or that
![]() $X$
admits an ample invertible sheaf
$X$
admits an ample invertible sheaf
![]() ${\mathcal{L}}$
with
${\mathcal{L}}$
with
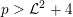 $p>{\mathcal{L}}^{2}+4$
. Then
$p>{\mathcal{L}}^{2}+4$
. Then
![]() $X$
satisfies Assumption
$X$
satisfies Assumption
![]() $(\star )$
.
$(\star )$
.
1.4 K3 surfaces
In this article, we establish a Néron–Ogg–Shafarevich–Serre–Tate type result for K3 surfaces. Important steps were already taken by the second named author in [Reference MatsumotoMat15]. Over the complex numbers, similar results are classically known; see, for example, [Reference Kulikov and KurchanovKK98, ch. 5].
Before coming to the main result of this article, we define a K3 surface with at worst RDP (rational double point) singularities to be a proper surface over a field, which, after base change to an algebraically closed field, has at worst rational double point singularities, and whose minimal resolution of singularities is a K3 surface.
Theorem 1.3. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
. If the
$(\star )$
. If the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
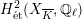 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for some
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for some
![]() $\ell \neq p$
, then the following hold.
$\ell \neq p$
, then the following hold.
-
(i) There exists a model of
 $X$
that is a projective scheme over
$X$
that is a projective scheme over
 ${\mathcal{O}}_{K}$
, whose special fiber is a K3 surface with at worst RDP singularities.
${\mathcal{O}}_{K}$
, whose special fiber is a K3 surface with at worst RDP singularities. -
(ii) Moreover, there exists an integer
 $N$
, independent of
$N$
, independent of
 $X$
and
$X$
and
 $K$
, and a finite unramified extension
$K$
, and a finite unramified extension
 $L/K$
of degree at most
$L/K$
of degree at most
 $N$
, such that
$N$
, such that
 $X_{L}$
has good reduction over
$X_{L}$
has good reduction over
 $L$
.
$L$
.
In [Reference Hassett and TschinkelHT17, Theorem 35], a similar result is obtained for K3 surfaces over
![]() $\mathbb{C}((t))$
, but their proof uses methods different from ours. As in the case of Abelian varieties in [Reference Serre and TateST68], we obtain the following independence of
$\mathbb{C}((t))$
, but their proof uses methods different from ours. As in the case of Abelian varieties in [Reference Serre and TateST68], we obtain the following independence of
![]() $\ell$
.
$\ell$
.
Corollary 1.4. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
. Then the
$(\star )$
. Then the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
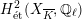 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
![]() $\ell \neq p$
if and only if it is unramified for all
$\ell \neq p$
if and only if it is unramified for all
![]() $\ell \neq p$
.
$\ell \neq p$
.
In [Reference Serre and TateST68], Serre and Tate showed that if an Abelian variety of dimension
![]() $g$
over
$g$
over
![]() $K$
with
$K$
with
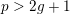 $p>2g+1$
has potential good reduction, then good reduction can be achieved after a tame extension. Here, we establish the following analog for K3 surfaces.
$p>2g+1$
has potential good reduction, then good reduction can be achieved after a tame extension. Here, we establish the following analog for K3 surfaces.
Corollary 1.5. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
with
$K$
with
![]() $p\geqslant 23$
and potential good reduction. Then
$p\geqslant 23$
and potential good reduction. Then
![]() $X$
has good reduction after a tame extension of
$X$
has good reduction after a tame extension of
![]() $K$
.
$K$
.
It is important to note that in part (2) of Theorem 1.3, we cannot avoid field extensions in general. More precisely, we construct the following explicit examples.
Theorem 1.6. For every prime
![]() $p\geqslant 5$
, there exists a K3 surface
$p\geqslant 5$
, there exists a K3 surface
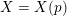 $X=X(p)$
over
$X=X(p)$
over
![]() $\mathbb{Q}_{p}$
, such that:
$\mathbb{Q}_{p}$
, such that:
-
(i) the
 $G_{\mathbb{Q}_{p}}$
-representation on
$G_{\mathbb{Q}_{p}}$
-representation on
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
 $\ell \neq p$
;
$\ell \neq p$
; -
(ii)
 $X$
has good reduction over the unramified extension
$X$
has good reduction over the unramified extension
 $\mathbb{Q}_{p^{2}}$
; but
$\mathbb{Q}_{p^{2}}$
; but -
(iii)
 $X$
does not have good reduction over
$X$
does not have good reduction over
 $\mathbb{Q}_{p}$
.
$\mathbb{Q}_{p}$
.
1.5 Kuga–Satake Abelian varieties
Let us recall that Kuga and Satake [Reference Kuga and SatakeKS67] associated to a polarized K3 surface
![]() $(X,{\mathcal{L}})$
over
$(X,{\mathcal{L}})$
over
![]() $\mathbb{C}$
a polarized Abelian variety
$\mathbb{C}$
a polarized Abelian variety
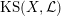 $\operatorname{KS}(X,{\mathcal{L}})$
of dimension
$\operatorname{KS}(X,{\mathcal{L}})$
of dimension
![]() $2^{19}$
over
$2^{19}$
over
![]() $\mathbb{C}$
. Moreover, if
$\mathbb{C}$
. Moreover, if
![]() $(X,{\mathcal{L}})$
is defined over an arbitrary field
$(X,{\mathcal{L}})$
is defined over an arbitrary field
![]() $k$
, then Rizov [Reference RizovRiz10] and Madapusi Pera [Reference Madapusi PeraMad15], building on work of Deligne [Reference DeligneDel72] and André [Reference AndréAnd96], established the existence of
$k$
, then Rizov [Reference RizovRiz10] and Madapusi Pera [Reference Madapusi PeraMad15], building on work of Deligne [Reference DeligneDel72] and André [Reference AndréAnd96], established the existence of
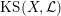 $\operatorname{KS}(X,{\mathcal{L}})$
over some finite extension of
$\operatorname{KS}(X,{\mathcal{L}})$
over some finite extension of
![]() $k$
. As an application of Theorem 1.3, we can compare the reduction behavior of a polarized K3 surface to that of its associated Kuga–Satake Abelian variety.
$k$
. As an application of Theorem 1.3, we can compare the reduction behavior of a polarized K3 surface to that of its associated Kuga–Satake Abelian variety.
Theorem 1.7. Assume
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $(X,{\mathcal{L}})$
be a polarized K3 surface over
$(X,{\mathcal{L}})$
be a polarized K3 surface over
![]() $K$
.
$K$
.
-
(i) If
 $X$
has good reduction, then
$X$
has good reduction, then
 $\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
$\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
 $L/K$
, and it has good reduction over
$L/K$
, and it has good reduction over
 $L$
.
$L$
. -
(ii) Assume that
 $X$
satisfies Assumption
$X$
satisfies Assumption
 $(\star )$
. Let
$(\star )$
. Let
 $L/K$
be a field extension such that both
$L/K$
be a field extension such that both
 $\operatorname{KS}(X,{\mathcal{L}})$
and the Kuga–Satake correspondence can be defined over
$\operatorname{KS}(X,{\mathcal{L}})$
and the Kuga–Satake correspondence can be defined over
 $L$
. If
$L$
. If
 $\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
$\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
 $L$
, then
$L$
, then
 $X$
has good reduction over an unramified extension of
$X$
has good reduction over an unramified extension of
 $L$
.
$L$
.
1.6 Organization
This article is organized as follows.
In § 2, we recall a couple of general facts on models and unramified Galois representations on
![]() $\ell$
-adic cohomology. We also recall the classical Serre–Tate theorem for Abelian varieties and give explicit examples of curves of genus at least
$\ell$
-adic cohomology. We also recall the classical Serre–Tate theorem for Abelian varieties and give explicit examples of curves of genus at least
![]() $2$
, where the Galois representation does not detect bad reduction.
$2$
, where the Galois representation does not detect bad reduction.
In § 3, we review potential semi-stable reduction of K3 surfaces, Kawamata’s semi-stable MMP, the Kulikov–Nakkajima–Pinkham–Persson classification list, and the second named author’s results on potential good reduction of K3 surfaces. We also briefly discuss potential good and semi-stable reduction of Enriques surfaces.
In § 4, we establish existence and termination of certain flops, which we need later on to equip our models with suitable invertible sheaves. Moreover, we show that any two smooth models of a K3 surface
![]() $X$
over
$X$
over
![]() $K$
are related by a finite sequence of flopping contractions and their inverses.
$K$
are related by a finite sequence of flopping contractions and their inverses.
Section 5 is the technical heart of this article: given a K3 surface
![]() $X$
over
$X$
over
![]() $K$
, a finite Galois extension
$K$
, a finite Galois extension
![]() $L/K$
with group
$L/K$
with group
![]() $G$
, and a model of
$G$
, and a model of
![]() $X_{L}$
over
$X_{L}$
over
![]() ${\mathcal{O}}_{L}$
, we study extensions of the
${\mathcal{O}}_{L}$
, we study extensions of the
![]() $G$
-action
$G$
-action
![]() $X_{L}$
to this model. Then we study quotients of such models by
$X_{L}$
to this model. Then we study quotients of such models by
![]() $G$
-actions, where the most difficult case arises when
$G$
-actions, where the most difficult case arises when
![]() $p$
divides the order of
$p$
divides the order of
![]() $G$
(wild action).
$G$
(wild action).
In § 6, we establish the main results of this article: a Néron–Ogg–Shafarevich type theorem for K3 surfaces, good reduction over tame extensions, as well as the connection to Kuga–Satake Abelian varieties.
Finally, in § 7, we give explicit examples of K3 surfaces over
![]() $\mathbb{Q}_{p}$
with unramified Galois representations on their
$\mathbb{Q}_{p}$
with unramified Galois representations on their
![]() $\ell$
-adic cohomology groups that do not have good reduction over
$\ell$
-adic cohomology groups that do not have good reduction over
![]() $\mathbb{Q}_{p}$
.
$\mathbb{Q}_{p}$
.
Notation and conventions
Throughout the whole article, we fix the following notation:
 $$\begin{eqnarray}\begin{array}{@{}ll@{}}{\mathcal{O}}_{K} & \text{a local Henselian DVR of characteristic zero;}\\ K & \text{its field of fractions;}\\ k & \text{the residue field, which we assume to be perfect;}\\ p\geqslant 0 & \text{the characteristic of }k;\\ \ell & \text{a prime different from }p;\\ G_{K},G_{k} & \text{the absolute Galois groups }\operatorname{Gal}(\overline{K}/K),\operatorname{Gal}(\overline{k}/k).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ll@{}}{\mathcal{O}}_{K} & \text{a local Henselian DVR of characteristic zero;}\\ K & \text{its field of fractions;}\\ k & \text{the residue field, which we assume to be perfect;}\\ p\geqslant 0 & \text{the characteristic of }k;\\ \ell & \text{a prime different from }p;\\ G_{K},G_{k} & \text{the absolute Galois groups }\operatorname{Gal}(\overline{K}/K),\operatorname{Gal}(\overline{k}/k).\end{array}\end{eqnarray}$$
If
![]() $L/K$
is a field extension, and
$L/K$
is a field extension, and
![]() $X$
is a scheme over
$X$
is a scheme over
![]() $K$
, we abbreviate the base-change
$K$
, we abbreviate the base-change
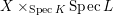 $X\times _{\operatorname{Spec}K}\operatorname{Spec}L$
by
$X\times _{\operatorname{Spec}K}\operatorname{Spec}L$
by
![]() $X_{L}$
.
$X_{L}$
.
2 Generalities
In this section, we recall a couple of general facts on models of varieties, unramified Galois representations on
![]() $\ell$
-adic cohomology groups, and Néron–Ogg–Shafarevich type theorems.
$\ell$
-adic cohomology groups, and Néron–Ogg–Shafarevich type theorems.
2.1 Models
We start with the definition of various types of models.
Definition 2.1. Let
![]() $X$
be a smooth and proper variety over
$X$
be a smooth and proper variety over
![]() $K$
.
$K$
.
-
(i) A model of
 $X$
over
$X$
over
 ${\mathcal{O}}_{K}$
is an algebraic space that is flat and proper over
${\mathcal{O}}_{K}$
is an algebraic space that is flat and proper over
 $\operatorname{Spec}{\mathcal{O}}_{K}$
and whose generic fiber is isomorphic to
$\operatorname{Spec}{\mathcal{O}}_{K}$
and whose generic fiber is isomorphic to
 $X$
.
$X$
. -
(ii) We say that
 $X$
has good reduction if there exists a model of
$X$
has good reduction if there exists a model of
 $X$
that is smooth over
$X$
that is smooth over
 ${\mathcal{O}}_{K}$
.
${\mathcal{O}}_{K}$
. -
(iii) We say that
 $X$
has semi-stable reduction if there exists a regular model of
$X$
has semi-stable reduction if there exists a regular model of
 $X$
, whose geometric special fiber is a reduced normal crossing divisor with smooth components. (Sometimes, this notion is also called strictly semi-stable reduction.)
$X$
, whose geometric special fiber is a reduced normal crossing divisor with smooth components. (Sometimes, this notion is also called strictly semi-stable reduction.) -
(iv) We say that
 $X$
has potential good (respectively semi-stable) reduction if there exists a finite field extension
$X$
has potential good (respectively semi-stable) reduction if there exists a finite field extension
 $L/K$
such that
$L/K$
such that
 $X_{L}$
has good (respectively semi-stable) reduction.
$X_{L}$
has good (respectively semi-stable) reduction.
Remark 2.2. Models of curves and Abelian varieties can be treated entirely within the category of schemes; see, for example, [Reference LiuLiu02, ch. 10] and [Reference Bosch, Lütkebohmert and RaynaudBLR90]. However, if
![]() $X$
is a K3 surface over
$X$
is a K3 surface over
![]() $K$
with good reduction, then it may not be possible to find a smooth model in the category of schemes, and we refer to [Reference MatsumotoMat15, §5.2] for explicit examples. In particular, we are forced to work with algebraic spaces when studying models of K3 surfaces.
$K$
with good reduction, then it may not be possible to find a smooth model in the category of schemes, and we refer to [Reference MatsumotoMat15, §5.2] for explicit examples. In particular, we are forced to work with algebraic spaces when studying models of K3 surfaces.
2.2 Inertia and monodromy
The
![]() $G_{K}$
-action on
$G_{K}$
-action on
![]() $\overline{K}$
induces an action on
$\overline{K}$
induces an action on
![]() ${\mathcal{O}}_{\overline{K}}$
and by reduction, an action on
${\mathcal{O}}_{\overline{K}}$
and by reduction, an action on
![]() $\overline{k}$
. This gives rise to a continuous and surjective homomorphism
$\overline{k}$
. This gives rise to a continuous and surjective homomorphism
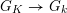 $G_{K}\rightarrow G_{k}$
of profinite groups. Thus we obtain a short exact sequence
$G_{K}\rightarrow G_{k}$
of profinite groups. Thus we obtain a short exact sequence
 $$\begin{eqnarray}1\rightarrow I_{K}\rightarrow G_{K}\rightarrow G_{k}\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow I_{K}\rightarrow G_{K}\rightarrow G_{k}\rightarrow 1,\end{eqnarray}$$
whose kernel
![]() $I_{K}$
is called the inertia group. In fact,
$I_{K}$
is called the inertia group. In fact,
![]() $I_{K}$
is the absolute Galois group of the maximal unramified extension of
$I_{K}$
is the absolute Galois group of the maximal unramified extension of
![]() $K$
. If
$K$
. If
![]() $p\neq 0$
, then the wild inertia group
$p\neq 0$
, then the wild inertia group
![]() $P_{K}$
is the normal subgroup of
$P_{K}$
is the normal subgroup of
![]() $G_{K}$
that is the absolute Galois group of the maximal tame extension of
$G_{K}$
that is the absolute Galois group of the maximal tame extension of
![]() $K$
. We note that
$K$
. We note that
![]() $P_{K}$
is the unique
$P_{K}$
is the unique
![]() $p$
-Sylow subgroup of
$p$
-Sylow subgroup of
![]() $I_{K}$
.
$I_{K}$
.
Definition 2.3. Let
![]() $X$
be a smooth and proper variety over
$X$
be a smooth and proper variety over
![]() $K$
. Then the
$K$
. Then the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
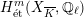 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is called unramified if
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is called unramified if
![]() $I_{K}$
acts trivially. It is called tame if
$I_{K}$
acts trivially. It is called tame if
![]() $P_{K}$
acts trivially.
$P_{K}$
acts trivially.
For an Abelian variety
![]() $X$
, it follows from results of Serre and Tate [Reference Serre and TateST68] that the
$X$
, it follows from results of Serre and Tate [Reference Serre and TateST68] that the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
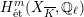 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
![]() $\ell \neq p$
, if and only if it is so for all
$\ell \neq p$
, if and only if it is so for all
![]() $\ell \neq p$
. In Corollary 6.4, we will show a similar result for K3 surfaces. In general, it is not known whether being unramified depends on the choice of
$\ell \neq p$
. In Corollary 6.4, we will show a similar result for K3 surfaces. In general, it is not known whether being unramified depends on the choice of
![]() $\ell$
, but it is expected not to.
$\ell$
, but it is expected not to.
A relation between good reduction and unramified Galois representations on
![]() $\ell$
-adic cohomology groups is given by the following well-known result, which follows from the proper smooth base change theorem. For schemes, it is stated in [Reference GrothendieckSGA4, Théorème XII.5.1], and in case the model is an algebraic space, we refer to [Reference Liu and ZhengLZ14, Theorem 0.1.1] or [Reference ArtinArt73, ch. VII].
$\ell$
-adic cohomology groups is given by the following well-known result, which follows from the proper smooth base change theorem. For schemes, it is stated in [Reference GrothendieckSGA4, Théorème XII.5.1], and in case the model is an algebraic space, we refer to [Reference Liu and ZhengLZ14, Theorem 0.1.1] or [Reference ArtinArt73, ch. VII].
Theorem 2.4. If
![]() $X$
has good reduction, then the
$X$
has good reduction, then the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
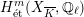 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
![]() $m$
and for all
$m$
and for all
![]() $\ell \neq p$
.
$\ell \neq p$
.
In view of this theorem, it is natural to ask for the converse direction. Whenever such a converse holds for some class of varieties over
![]() $K$
, we obtain a purely representation-theoretic criterion to determine whether such a variety admits a model over
$K$
, we obtain a purely representation-theoretic criterion to determine whether such a variety admits a model over
![]() ${\mathcal{O}}_{K}$
with good reduction.
${\mathcal{O}}_{K}$
with good reduction.
2.3 Abelian varieties
A classical converse to Theorem 2.4 is the Néron–Ogg–Shafarevich criterion for elliptic curves. Later, Serre and Tate generalized it to Abelian varieties of arbitrary dimension.
Theorem 2.5 (Serre–Tate [Reference Serre and TateST68]).
An Abelian variety
![]() $A$
over
$A$
over
![]() $K$
has good reduction if and only if the
$K$
has good reduction if and only if the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
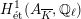 $H_{\acute{\text{e}}\text{t}}^{1}(A_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one (respectively all)
$H_{\acute{\text{e}}\text{t}}^{1}(A_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one (respectively all)
![]() $\ell \neq p$
.
$\ell \neq p$
.
2.4 Higher genus curves, part 1
Now, the converse to Theorem 2.4 already fails for curves of higher genus. Let
![]() $X$
be a smooth and proper curve of genus
$X$
be a smooth and proper curve of genus
![]() $g\geqslant 2$
over
$g\geqslant 2$
over
![]() $K$
. Let
$K$
. Let
![]() $\operatorname{Jac}(X)$
be its Jacobian, which is an Abelian variety of dimension
$\operatorname{Jac}(X)$
be its Jacobian, which is an Abelian variety of dimension
![]() $g$
over
$g$
over
![]() $K$
. Then the exact sequence of étale sheaves on
$K$
. Then the exact sequence of étale sheaves on
![]() $X$
$X$
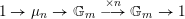 $$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D707}_{n}\rightarrow \mathbb{G}_{m}\stackrel{\times n}{\longrightarrow }\mathbb{G}_{m}\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D707}_{n}\rightarrow \mathbb{G}_{m}\stackrel{\times n}{\longrightarrow }\mathbb{G}_{m}\rightarrow 1\end{eqnarray}$$
gives rise to
![]() $G_{K}$
-equivariant isomorphisms
$G_{K}$
-equivariant isomorphisms
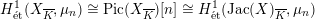 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\unicode[STIX]{x1D707}_{n})\cong \operatorname{Pic}(X_{\overline{K}})[n]\cong H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{Jac}(X)_{\overline{K}},\unicode[STIX]{x1D707}_{n})$
, from which we obtain
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\unicode[STIX]{x1D707}_{n})\cong \operatorname{Pic}(X_{\overline{K}})[n]\cong H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{Jac}(X)_{\overline{K}},\unicode[STIX]{x1D707}_{n})$
, from which we obtain
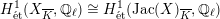 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })\cong H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{Jac}(X)_{\overline{K}},\mathbb{Q}_{\ell })$
by passing to the limit. Moreover, if
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })\cong H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{Jac}(X)_{\overline{K}},\mathbb{Q}_{\ell })$
by passing to the limit. Moreover, if
![]() $X$
has a
$X$
has a
![]() $K$
-rational point, then there is a natural embedding
$K$
-rational point, then there is a natural embedding
 $$\begin{eqnarray}j:X\rightarrow \operatorname{Jac}(X),\end{eqnarray}$$
$$\begin{eqnarray}j:X\rightarrow \operatorname{Jac}(X),\end{eqnarray}$$
and the above isomorphism coincides with
![]() $j^{\ast }$
(which is independent of the choice of a rational point). By the Serre–Tate theorem (Theorem 2.5), an unramified
$j^{\ast }$
(which is independent of the choice of a rational point). By the Serre–Tate theorem (Theorem 2.5), an unramified
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
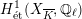 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is equivalent to good reduction of
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is equivalent to good reduction of
![]() $\operatorname{Jac}(X)$
. The following lemma gives a criterion that ensures the latter.
$\operatorname{Jac}(X)$
. The following lemma gives a criterion that ensures the latter.
Lemma 2.6. Let
![]() $X$
be a smooth and proper curve over
$X$
be a smooth and proper curve over
![]() $K$
that admits a semi-stable scheme model
$K$
that admits a semi-stable scheme model
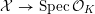 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
such that the dual graph associated to the components of its special fiber
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
such that the dual graph associated to the components of its special fiber
![]() ${\mathcal{X}}_{0}$
is a tree. Then
${\mathcal{X}}_{0}$
is a tree. Then
![]() $\operatorname{Jac}(X)$
has good reduction and the
$\operatorname{Jac}(X)$
has good reduction and the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
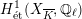 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.
Proof. By [Reference Bosch, Lütkebohmert and RaynaudBLR90, §9.2, Example 8],
![]() $\operatorname{Pic}_{{\mathcal{X}}_{0}/k}^{0}$
is an Abelian variety, which implies that
$\operatorname{Pic}_{{\mathcal{X}}_{0}/k}^{0}$
is an Abelian variety, which implies that
![]() $\operatorname{Jac}(X)$
has good reduction, and thus the
$\operatorname{Jac}(X)$
has good reduction, and thus the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
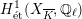 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.◻
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified.◻
Using this lemma, it is easy to produce counterexamples to Néron–Ogg–Shafarevich type results for curves of higher genus.
Proposition 2.7. If
![]() $p\neq 2$
, then there exists for infinitely many
$p\neq 2$
, then there exists for infinitely many
![]() $g\geqslant 2$
a smooth and proper curve
$g\geqslant 2$
a smooth and proper curve
![]() $X$
of genus
$X$
of genus
![]() $g$
over
$g$
over
![]() $K$
such that:
$K$
such that:
-
(i) the
 $G_{K}$
-representation on
$G_{K}$
-representation on
 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
 $m$
and all
$m$
and all
 $\ell \neq p$
; and
$\ell \neq p$
; and -
(ii)
 $X$
does not have good reduction over
$X$
does not have good reduction over
 $K$
nor over any finite extension.
$K$
nor over any finite extension.
Proof. We give examples for
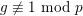 $g\not \equiv 1~\text{mod}~p$
. Let
$g\not \equiv 1~\text{mod}~p$
. Let
![]() $X$
be a hyperelliptic curve of genus
$X$
be a hyperelliptic curve of genus
![]() $g$
over
$g$
over
![]() $K$
that is one of the examples of [Reference LiuLiu02, Example 10.1.30] with the extra assumptions of [Reference LiuLiu02, Example 10.3.46] (here, we need the assumption
$K$
that is one of the examples of [Reference LiuLiu02, Example 10.1.30] with the extra assumptions of [Reference LiuLiu02, Example 10.3.46] (here, we need the assumption
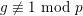 $g\not \equiv 1~\text{mod}~p$
). Then
$g\not \equiv 1~\text{mod}~p$
). Then
![]() $X$
has stable reduction over
$X$
has stable reduction over
![]() $K$
, as well as over every finite extension field
$K$
, as well as over every finite extension field
![]() $L/K$
. In this example, the special fiber of the stable model is the union of a curve of genus
$L/K$
. In this example, the special fiber of the stable model is the union of a curve of genus
![]() $1$
and a curve of genus
$1$
and a curve of genus
![]() $(g-1)$
meeting transversally in one point. In particular, neither
$(g-1)$
meeting transversally in one point. In particular, neither
![]() $X$
nor any base-change
$X$
nor any base-change
![]() $X_{L}$
have good reduction, but since the assumptions of Lemma 2.6 are fulfilled, the
$X_{L}$
have good reduction, but since the assumptions of Lemma 2.6 are fulfilled, the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
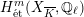 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
![]() $m$
and all
$m$
and all
![]() $\ell \neq p$
.◻
$\ell \neq p$
.◻
We stress that these results are well known to the experts, but since we were not able to find explicit references and explicit examples, we decided to include them here.
2.5 Higher genus curves, part 2
If
![]() $X$
is a smooth and proper curve of genus at least
$X$
is a smooth and proper curve of genus at least
![]() $2$
over
$2$
over
![]() $K$
, then one can also study the outer
$K$
, then one can also study the outer
![]() $G_{K}$
-representation on its étale fundamental group, which turns out to detect good reduction. More precisely, there exists a short exact sequence of étale fundamental groups
$G_{K}$
-representation on its étale fundamental group, which turns out to detect good reduction. More precisely, there exists a short exact sequence of étale fundamental groups
 $$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})\rightarrow \unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)\rightarrow G_{K}\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})\rightarrow \unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)\rightarrow G_{K}\rightarrow 1.\end{eqnarray}$$
For every prime
![]() $\ell$
, this exact sequence gives rise to a well-defined homomorphism from
$\ell$
, this exact sequence gives rise to a well-defined homomorphism from
![]() $G_{K}$
to the outer automorphism group of the pro-
$G_{K}$
to the outer automorphism group of the pro-
![]() $\ell$
-completion
$\ell$
-completion
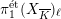 $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }$
of the geometric étale fundamental group
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }$
of the geometric étale fundamental group
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:G_{K}\longrightarrow \operatorname{Out}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:G_{K}\longrightarrow \operatorname{Out}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }).\end{eqnarray}$$
In analogy to Definition 2.3, we will say that this representation is unramified if
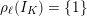 $\unicode[STIX]{x1D70C}_{\ell }(I_{K})=\{1\}$
. We note that the
$\unicode[STIX]{x1D70C}_{\ell }(I_{K})=\{1\}$
. We note that the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
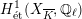 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
arises from the residual action of
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{K}},\mathbb{Q}_{\ell })$
arises from the residual action of
![]() $\unicode[STIX]{x1D70C}_{\ell }$
on the Abelianization of
$\unicode[STIX]{x1D70C}_{\ell }$
on the Abelianization of
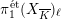 $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }$
. After these preparations, we have the following Néron–Ogg–Shafarevich type theorem for curves of higher genus, which is in terms of fundamental groups rather than cohomology groups.
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X_{\overline{K}})_{\ell }$
. After these preparations, we have the following Néron–Ogg–Shafarevich type theorem for curves of higher genus, which is in terms of fundamental groups rather than cohomology groups.
Theorem 2.8 (Oda [Reference OdaOda95, Theorem 3.2]).
Let
![]() $X$
be a smooth and proper curve of genus at least
$X$
be a smooth and proper curve of genus at least
![]() $2$
over
$2$
over
![]() $K$
. Then
$K$
. Then
![]() $X$
has good reduction if and only if the outer Galois action
$X$
has good reduction if and only if the outer Galois action
![]() $\unicode[STIX]{x1D70C}_{\ell }$
is unramified for one (respectively all)
$\unicode[STIX]{x1D70C}_{\ell }$
is unramified for one (respectively all)
![]() $\ell \neq p$
.
$\ell \neq p$
.
3 K3 surfaces and their models
In this section, we first introduce the crucial Assumption
![]() $(\star )$
, which ensures the existence of suitable models for K3 surfaces. These models have been studied by Kulikov, Nakkajima, Persson, and Pinkham. Following ideas of Maulik, we show how Assumption
$(\star )$
, which ensures the existence of suitable models for K3 surfaces. These models have been studied by Kulikov, Nakkajima, Persson, and Pinkham. Following ideas of Maulik, we show how Assumption
![]() $(\star )$
would follow from a combination of potential semi-stable reduction (which is not known in mixed characteristic, but expected) and the semi-stable minimal model program (MMP) in mixed characteristic. Then we give some conditions under which Assumption
$(\star )$
would follow from a combination of potential semi-stable reduction (which is not known in mixed characteristic, but expected) and the semi-stable minimal model program (MMP) in mixed characteristic. Then we give some conditions under which Assumption
![]() $(\star )$
does hold. After that, we shortly review the second named author’s results on potential good reduction of K3 surfaces. Finally, we show by example that these results do not carry over to Enriques surfaces. Most of the results of this section are probably known to the experts.
$(\star )$
does hold. After that, we shortly review the second named author’s results on potential good reduction of K3 surfaces. Finally, we show by example that these results do not carry over to Enriques surfaces. Most of the results of this section are probably known to the experts.
3.1 Kulikov–Nakkajima–Persson–Pinkham models
We first introduce the crucial assumption that we shall make from now on.
Assumption
 $(\star )$
.
$(\star )$
.
A K3 surface
![]() $X$
over
$X$
over
![]() $K$
satisfies Assumption (
$K$
satisfies Assumption (
![]() $\star$
) if there exists a finite field extension
$\star$
) if there exists a finite field extension
![]() $L/K$
such that
$L/K$
such that
![]() $X_{L}$
admits a semi-stable model
$X_{L}$
admits a semi-stable model
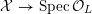 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
(in the sense of Definition 2.1) such that
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
(in the sense of Definition 2.1) such that
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
is trivial.
$\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
is trivial.
Here, we equip
![]() ${\mathcal{X}}$
with its standard log structure
${\mathcal{X}}$
with its standard log structure
![]() ${\mathcal{X}}^{\log }$
and define the relative canonical sheaf
${\mathcal{X}}^{\log }$
and define the relative canonical sheaf
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
to be
$\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
to be
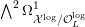 $\bigwedge ^{2}\unicode[STIX]{x1D6FA}_{{\mathcal{X}}^{\log }/{\mathcal{O}}_{L}^{\log }}^{1}$
using log differentials. Since
$\bigwedge ^{2}\unicode[STIX]{x1D6FA}_{{\mathcal{X}}^{\log }/{\mathcal{O}}_{L}^{\log }}^{1}$
using log differentials. Since
![]() ${\mathcal{X}}^{\log }$
is log smooth over
${\mathcal{X}}^{\log }$
is log smooth over
![]() ${\mathcal{O}}_{L}$
, the sheaf
${\mathcal{O}}_{L}$
, the sheaf
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
is invertible; see also the discussion in [Reference MatsumotoMat15, §3].
$\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{L}}$
is invertible; see also the discussion in [Reference MatsumotoMat15, §3].
The main reason why Assumption
![]() $(\star )$
is not known to hold is that potential semi-stable reduction is not known: using resolution of singularities in mixed characteristic (recently announced by Cossart and Piltant [Reference Cossart and PiltantCP14]) and embedded resolution of singularities (Cossart et al. [Reference Cossart, Jannsen and SaitoCJS13]), we obtain a model
$(\star )$
is not known to hold is that potential semi-stable reduction is not known: using resolution of singularities in mixed characteristic (recently announced by Cossart and Piltant [Reference Cossart and PiltantCP14]) and embedded resolution of singularities (Cossart et al. [Reference Cossart, Jannsen and SaitoCJS13]), we obtain a model
![]() ${\mathcal{X}}$
, whose special fiber
${\mathcal{X}}$
, whose special fiber
![]() ${\mathcal{X}}_{0}$
has simple normal crossing support, but whose components may have multiplicities. At the moment, it is not clear how to get rid of these multiplicities after base change, unless all of them are prime to
${\mathcal{X}}_{0}$
has simple normal crossing support, but whose components may have multiplicities. At the moment, it is not clear how to get rid of these multiplicities after base change, unless all of them are prime to
![]() $p$
. In case the residue characteristic is zero, these results are classically known to hold; see the discussion in [Reference Kollár and MoriKM98, §7.2] for details.
$p$
. In case the residue characteristic is zero, these results are classically known to hold; see the discussion in [Reference Kollár and MoriKM98, §7.2] for details.
The following result, which is inspired by Maulik’s approach and ideas from [Reference MaulikMau14, §4], shows that Assumption
![]() $(\star )$
essentially holds once we assume potential semi-stable reduction. More precisely, we have the following.
$(\star )$
essentially holds once we assume potential semi-stable reduction. More precisely, we have the following.
Proposition 3.1. Assume
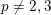 $p\neq 2,3$
. Let
$p\neq 2,3$
. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
and assume that there exists:
$K$
and assume that there exists:
-
(i) a finite field extension
 $L^{\prime }/K$
; and
$L^{\prime }/K$
; and -
(ii) a smooth surface
 $Y$
over
$Y$
over
 $L^{\prime }$
that is birationally equivalent to
$L^{\prime }$
that is birationally equivalent to
 $X_{L^{\prime }}$
; and
$X_{L^{\prime }}$
; and -
(iii) a scheme model
 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
of
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
of
 $Y$
with semi-stable reduction.
$Y$
with semi-stable reduction.
Then
![]() $X$
satisfies Assumption
$X$
satisfies Assumption
![]() $(\star )$
.
$(\star )$
.
Proof. Let
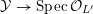 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
be as in the statement. Since
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
be as in the statement. Since
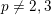 $p\neq 2,3$
, Kawamata’s semi-stable MMP [Reference KawamataKaw94] (see also [Reference Kollár and MoriKM98, §7.1] for
$p\neq 2,3$
, Kawamata’s semi-stable MMP [Reference KawamataKaw94] (see also [Reference Kollár and MoriKM98, §7.1] for
![]() $p=0$
) produces a scheme
$p=0$
) produces a scheme
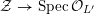 ${\mathcal{Z}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
with nef relative canonical divisor
${\mathcal{Z}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L^{\prime }}$
with nef relative canonical divisor
![]() $K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
that is a model of a smooth proper surface birationally equivalent to
$K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
that is a model of a smooth proper surface birationally equivalent to
![]() $X_{L^{\prime }}$
, and such that
$X_{L^{\prime }}$
, and such that
![]() ${\mathcal{Z}}$
is regular outside a finite set
${\mathcal{Z}}$
is regular outside a finite set
![]() $\unicode[STIX]{x1D6F4}$
of terminal singularities. We refer to [Reference KawamataKaw94, § 1] for details and the definition of
$\unicode[STIX]{x1D6F4}$
of terminal singularities. We refer to [Reference KawamataKaw94, § 1] for details and the definition of
![]() $K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
, which is a Weil divisor. We also note that it coincides with the Weil divisor class associated to the relative canonical divisor
$K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
, which is a Weil divisor. We also note that it coincides with the Weil divisor class associated to the relative canonical divisor
![]() $\unicode[STIX]{x1D714}_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
, see, for example, [Reference MatsumotoMat15, §3].
$\unicode[STIX]{x1D714}_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
, see, for example, [Reference MatsumotoMat15, §3].
Since
![]() $X_{L^{\prime }}$
is a minimal surface and
$X_{L^{\prime }}$
is a minimal surface and
![]() $K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is nef, the generic fiber of
$K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is nef, the generic fiber of
![]() ${\mathcal{Z}}$
is actually isomorphic to
${\mathcal{Z}}$
is actually isomorphic to
![]() $X_{L^{\prime }}$
, and it follows that
$X_{L^{\prime }}$
, and it follows that
![]() $K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is trivial. Outside
$K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is trivial. Outside
![]() $\unicode[STIX]{x1D6F4}$
, this model is already a semi-stable model. From the classification of terminal singularities in [Reference KawamataKaw94, Theorem 4.4] and the fact that
$\unicode[STIX]{x1D6F4}$
, this model is already a semi-stable model. From the classification of terminal singularities in [Reference KawamataKaw94, Theorem 4.4] and the fact that
![]() $K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is Cartier at points of
$K_{{\mathcal{Z}}/{\mathcal{O}}_{L^{\prime }}}$
is Cartier at points of
![]() $\unicode[STIX]{x1D6F4}$
(since it is trivial), it follows that the geometric special fiber
$\unicode[STIX]{x1D6F4}$
(since it is trivial), it follows that the geometric special fiber
![]() $({\mathcal{Z}}_{0})_{\overline{k}}$
is irreducible around points of
$({\mathcal{Z}}_{0})_{\overline{k}}$
is irreducible around points of
![]() $\unicode[STIX]{x1D6F4}$
, and that it acquires RDP singularities in these points. Thus, after some finite field extension
$\unicode[STIX]{x1D6F4}$
, and that it acquires RDP singularities in these points. Thus, after some finite field extension
![]() $L/L^{\prime }$
, there exists a simultaneous resolution
$L/L^{\prime }$
, there exists a simultaneous resolution
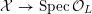 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of these singularities by [Reference ArtinArt74, Theorem 2]. This
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of these singularities by [Reference ArtinArt74, Theorem 2]. This
![]() ${\mathcal{X}}$
may exist only as an algebraic space, and it satisfies Assumption
${\mathcal{X}}$
may exist only as an algebraic space, and it satisfies Assumption
![]() $(\star )$
.◻
$(\star )$
.◻
As already mentioned above, the assumptions are fulfilled if
![]() $p=0$
; see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, ch. 2] or the discussion in [Reference Kollár and MoriKM98, §7.2]. If
$p=0$
; see [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, ch. 2] or the discussion in [Reference Kollár and MoriKM98, §7.2]. If
![]() $p\neq 0$
, then they are fulfilled for K3 surfaces that admit a very ample invertible sheaf
$p\neq 0$
, then they are fulfilled for K3 surfaces that admit a very ample invertible sheaf
![]() ${\mathcal{L}}$
with
${\mathcal{L}}$
with
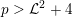 $p>{\mathcal{L}}^{2}+4$
by a result of Maulik [Reference MaulikMau14, §4]. With some extra work, the condition ‘very ample’ can be weakened to ‘ample’ (see [Reference MatsumotoMat15, argument following Lemma 3.1]) and Theorem 1.2 follows. Thus we have the following result.
$p>{\mathcal{L}}^{2}+4$
by a result of Maulik [Reference MaulikMau14, §4]. With some extra work, the condition ‘very ample’ can be weakened to ‘ample’ (see [Reference MatsumotoMat15, argument following Lemma 3.1]) and Theorem 1.2 follows. Thus we have the following result.
Theorem 3.2 (
 $=$
Theorem 1.2).
$=$
Theorem 1.2).
Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
and assume that
$K$
and assume that
![]() $p=0$
or that
$p=0$
or that
![]() $X$
admits an ample invertible sheaf
$X$
admits an ample invertible sheaf
![]() ${\mathcal{L}}$
with
${\mathcal{L}}$
with
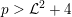 $p>{\mathcal{L}}^{2}+4$
. Then
$p>{\mathcal{L}}^{2}+4$
. Then
![]() $X$
satisfies Assumption
$X$
satisfies Assumption
![]() $(\star )$
.
$(\star )$
.
Over
![]() $\mathbb{C}$
, Kulikov [Reference KulikovKul77], Persson [Reference PerssonPer77], and Pinkham and Persson [Reference Persson and PinkhamPP81] classified the special fibers of the models asserted by Assumption
$\mathbb{C}$
, Kulikov [Reference KulikovKul77], Persson [Reference PerssonPer77], and Pinkham and Persson [Reference Persson and PinkhamPP81] classified the special fibers of the models asserted by Assumption
![]() $(\star )$
. We refer to [Reference MorrisonMor81, §1] and [Reference Kulikov and KurchanovKK98, ch. 5] for overview, and to Nakkajima’s extension [Reference NakkajimaNakk00] of these results to mixed characteristic.
$(\star )$
. We refer to [Reference MorrisonMor81, §1] and [Reference Kulikov and KurchanovKK98, ch. 5] for overview, and to Nakkajima’s extension [Reference NakkajimaNakk00] of these results to mixed characteristic.
3.2 Potential good reduction of K3 surfaces
Now, if
![]() $X$
is a K3 surface over
$X$
is a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
, then there exists a finite field extension
$(\star )$
, then there exists a finite field extension
![]() $L/K$
and a model
$L/K$
and a model
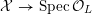 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
![]() $X_{L}$
as asserted by Assumption
$X_{L}$
as asserted by Assumption
![]() $(\star )$
. If the
$(\star )$
. If the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
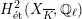 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified, then the weight filtration on
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified, then the weight filtration on
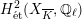 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
that arises from the Steenbrink–Rapoport–Zink spectral sequence (see [Reference SteenbrinkSte76], [Reference Rapoport and ZinkRZ82, Satz 2.10], and [Reference NakayamaNaka00, Proposition 1.9] for details) is trivial. Together with a result of Persson [Reference PerssonPer77, Proposition 3.3.6], this implies that the special fiber of
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
that arises from the Steenbrink–Rapoport–Zink spectral sequence (see [Reference SteenbrinkSte76], [Reference Rapoport and ZinkRZ82, Satz 2.10], and [Reference NakayamaNaka00, Proposition 1.9] for details) is trivial. Together with a result of Persson [Reference PerssonPer77, Proposition 3.3.6], this implies that the special fiber of
![]() ${\mathcal{X}}$
is smooth, that is,
${\mathcal{X}}$
is smooth, that is,
![]() $X_{L}$
has good reduction. Thus we obtain the following result of the second named author and we refer to [Reference MatsumotoMat15] for details and a detailed proof.
$X_{L}$
has good reduction. Thus we obtain the following result of the second named author and we refer to [Reference MatsumotoMat15] for details and a detailed proof.
Theorem 3.3 (Matsumoto).
Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
. If the
$(\star )$
. If the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
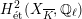 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
![]() $\ell \neq p$
, then
$\ell \neq p$
, then
![]() $X$
has potential good reduction.
$X$
has potential good reduction.
3.3 Enriques surfaces
The previous theorem does not generalize to other classes of surfaces with numerically trivial canonical sheaves. For example, the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
![]() $\ell$
-adic cohomology of an Enriques surface can neither exclude nor confirm any type in the Kulikov–Nakkajima–Persson–Pinkham list for these surfaces. More precisely, we have the following.
$\ell$
-adic cohomology of an Enriques surface can neither exclude nor confirm any type in the Kulikov–Nakkajima–Persson–Pinkham list for these surfaces. More precisely, we have the following.
Lemma 3.4. Let
![]() $Y$
be an Enriques surface over
$Y$
be an Enriques surface over
![]() $K$
. Then there exists a finite extension
$K$
. Then there exists a finite extension
![]() $L/K$
such that the
$L/K$
such that the
![]() $G_{L}$
-representation on
$G_{L}$
-representation on
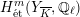 $H_{\acute{\text{e}}\text{t}}^{m}(Y_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{m}(Y_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for all
![]() $m$
and all
$m$
and all
![]() $\ell \neq p$
.
$\ell \neq p$
.
Proof. We only have to show something for
![]() $m=2$
. But then the first Chern class induces a
$m=2$
. But then the first Chern class induces a
![]() $G_{K}$
-equivariant isomorphism
$G_{K}$
-equivariant isomorphism
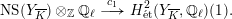 $$\begin{eqnarray}\operatorname{NS}(Y_{\overline{K}})\otimes _{\mathbb{Z}}\mathbb{Q}_{\ell }\stackrel{c_{1}}{\longrightarrow }H_{\acute{\text{e}}\text{t}}^{2}(Y_{\overline{K}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{NS}(Y_{\overline{K}})\otimes _{\mathbb{Z}}\mathbb{Q}_{\ell }\stackrel{c_{1}}{\longrightarrow }H_{\acute{\text{e}}\text{t}}^{2}(Y_{\overline{K}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
After passing to a finite extension
![]() $L/K$
, we may assume that
$L/K$
, we may assume that
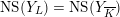 $\operatorname{NS}(Y_{L})=\operatorname{NS}(Y_{\overline{K}})$
. But then the
$\operatorname{NS}(Y_{L})=\operatorname{NS}(Y_{\overline{K}})$
. But then the
![]() $G_{L}$
-representation on
$G_{L}$
-representation on
![]() $\operatorname{NS}(Y_{L})$
is trivial; hence it is also trivial on
$\operatorname{NS}(Y_{L})$
is trivial; hence it is also trivial on
![]() $H_{\acute{\text{e}}\text{t}}^{2}$
, and, in particular, unramified.◻
$H_{\acute{\text{e}}\text{t}}^{2}$
, and, in particular, unramified.◻
Moreover, the next example shows that also the
![]() $G_{K}$
-representation on the
$G_{K}$
-representation on the
![]() $\ell$
-adic cohomology of the K3 double cover
$\ell$
-adic cohomology of the K3 double cover
![]() $X$
of an Enriques surface
$X$
of an Enriques surface
![]() $Y$
does not detect potential good reduction of
$Y$
does not detect potential good reduction of
![]() $Y$
. This phenomenon is related to flower pot degenerations of Enriques surfaces, see [Reference PerssonPer77, §3.3] and [Reference PerssonPer77, Appendix 2].
$Y$
. This phenomenon is related to flower pot degenerations of Enriques surfaces, see [Reference PerssonPer77, §3.3] and [Reference PerssonPer77, Appendix 2].
Example 3.5. Fix a prime
![]() $p\geqslant 5$
. Consider
$p\geqslant 5$
. Consider
![]() $\mathbb{P}_{\mathbb{Z}_{p}}^{5}$
with coordinates
$\mathbb{P}_{\mathbb{Z}_{p}}^{5}$
with coordinates
![]() $x_{i},y_{i}$
,
$x_{i},y_{i}$
,
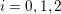 $i=0,1,2$
, and inside it the complete intersection of three quadrics
$i=0,1,2$
, and inside it the complete intersection of three quadrics
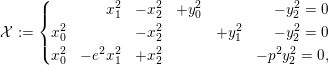 $$\begin{eqnarray}{\mathcal{X}}:=\left\{\begin{array}{@{}rrrrrr@{}} & x_{1}^{2} & -x_{2}^{2} & +y_{0}^{2} & & -y_{2}^{2}=0\\ x_{0}^{2} & & -x_{2}^{2} & & +y_{1}^{2} & -y_{2}^{2}=0\\ x_{0}^{2} & -e^{2}x_{1}^{2} & +x_{2}^{2} & & & -p^{2}y_{2}^{2}=0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}:=\left\{\begin{array}{@{}rrrrrr@{}} & x_{1}^{2} & -x_{2}^{2} & +y_{0}^{2} & & -y_{2}^{2}=0\\ x_{0}^{2} & & -x_{2}^{2} & & +y_{1}^{2} & -y_{2}^{2}=0\\ x_{0}^{2} & -e^{2}x_{1}^{2} & +x_{2}^{2} & & & -p^{2}y_{2}^{2}=0,\end{array}\right.\end{eqnarray}$$
where
![]() $e\in \mathbb{Z}_{p}^{\times }$
satisfies
$e\in \mathbb{Z}_{p}^{\times }$
satisfies
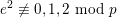 $e^{2}\not \equiv 0,1,2~\text{mod}~p$
(for example, we could take
$e^{2}\not \equiv 0,1,2~\text{mod}~p$
(for example, we could take
![]() $e=2$
). Then
$e=2$
). Then
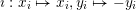 $\imath :x_{i}\mapsto x_{i},y_{i}\mapsto -y_{i}$
defines an involution on
$\imath :x_{i}\mapsto x_{i},y_{i}\mapsto -y_{i}$
defines an involution on
![]() $\mathbb{P}_{\mathbb{Z}_{p}}^{5}$
, which induces an involution on
$\mathbb{P}_{\mathbb{Z}_{p}}^{5}$
, which induces an involution on
![]() ${\mathcal{X}}$
. We denote by
${\mathcal{X}}$
. We denote by
![]() $X$
the generic fiber of
$X$
the generic fiber of
![]() ${\mathcal{X}}$
, and by
${\mathcal{X}}$
, and by
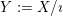 $Y:=X/\imath$
the quotient by the involution.
$Y:=X/\imath$
the quotient by the involution.
Theorem 3.6. Let
![]() $p\geqslant 5$
and let
$p\geqslant 5$
and let
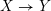 $X\rightarrow Y$
be as in Example 3.5. Then
$X\rightarrow Y$
be as in Example 3.5. Then
![]() $Y$
is an Enriques surface over
$Y$
is an Enriques surface over
![]() $\mathbb{Q}_{p}$
, such that:
$\mathbb{Q}_{p}$
, such that:
-
(i) the K3 double cover
 $X$
of
$X$
of
 $Y$
has good reduction;
$Y$
has good reduction; -
(ii) the
 $G_{\mathbb{Q}_{p}}$
-action on
$G_{\mathbb{Q}_{p}}$
-action on
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
 $\ell \neq p$
;
$\ell \neq p$
; -
(iii)
 $Y$
has semi-stable reduction of flower pot type; but
$Y$
has semi-stable reduction of flower pot type; but -
(iv)
 $Y$
does not have potential good reduction.
$Y$
does not have potential good reduction.
Proof. A straightforward computation shows that
![]() $X$
is smooth over
$X$
is smooth over
![]() $\mathbb{Q}_{p}$
, and that
$\mathbb{Q}_{p}$
, and that
![]() $\imath$
acts without fixed points on
$\imath$
acts without fixed points on
![]() $X$
. Thus
$X$
. Thus
![]() $X$
is a K3 surface and
$X$
is a K3 surface and
![]() $Y$
is an Enriques surface over
$Y$
is an Enriques surface over
![]() $\mathbb{Q}_{p}$
. The special fiber of
$\mathbb{Q}_{p}$
. The special fiber of
![]() ${\mathcal{X}}$
is a non-smooth K3 surface with four RDP singularities of type
${\mathcal{X}}$
is a non-smooth K3 surface with four RDP singularities of type
![]() $A_{1}$
located at
$A_{1}$
located at
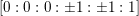 $[0:0:0:\pm 1:\pm 1:1]$
. Then the blow-up
$[0:0:0:\pm 1:\pm 1:1]$
. Then the blow-up
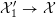 ${\mathcal{X}}_{1}^{\prime }\rightarrow {\mathcal{X}}$
of the Weil divisor
${\mathcal{X}}_{1}^{\prime }\rightarrow {\mathcal{X}}$
of the Weil divisor
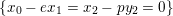 $\{x_{0}-ex_{1}=x_{2}-py_{2}=0\}$
defines a simultaneous resolution of the singularities of
$\{x_{0}-ex_{1}=x_{2}-py_{2}=0\}$
defines a simultaneous resolution of the singularities of
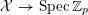 ${\mathcal{X}}\rightarrow \operatorname{Spec}\mathbb{Z}_{p}$
, and we obtain a smooth model of
${\mathcal{X}}\rightarrow \operatorname{Spec}\mathbb{Z}_{p}$
, and we obtain a smooth model of
![]() $X$
over
$X$
over
![]() $\mathbb{Z}_{p}$
. In particular,
$\mathbb{Z}_{p}$
. In particular,
![]() $X$
has good reduction over
$X$
has good reduction over
![]() $\mathbb{Q}_{p}$
and the
$\mathbb{Q}_{p}$
and the
![]() $G_{\mathbb{Q}_{p}}$
-representation on
$G_{\mathbb{Q}_{p}}$
-representation on
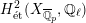 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
![]() $\ell \neq p$
.
$\ell \neq p$
.
Next, let
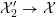 ${\mathcal{X}}_{2}^{\prime }\rightarrow {\mathcal{X}}$
be the blow-up of the four singular points of the special fiber. Then
${\mathcal{X}}_{2}^{\prime }\rightarrow {\mathcal{X}}$
be the blow-up of the four singular points of the special fiber. Then
![]() $\imath$
extends to
$\imath$
extends to
![]() ${\mathcal{X}}_{2}^{\prime }$
, and the special fiber is the union of four divisors
${\mathcal{X}}_{2}^{\prime }$
, and the special fiber is the union of four divisors
![]() $E_{i}$
with the minimal desingularization
$E_{i}$
with the minimal desingularization
![]() $X_{p}^{\prime }$
of the special fiber of
$X_{p}^{\prime }$
of the special fiber of
![]() ${\mathcal{X}}$
. The fixed locus of
${\mathcal{X}}$
. The fixed locus of
![]() $\imath$
on
$\imath$
on
![]() $X_{p}^{\prime }$
is the union of the four
$X_{p}^{\prime }$
is the union of the four
![]() $(-2)$
-curves of the resolution. Moreover, there exist isomorphisms
$(-2)$
-curves of the resolution. Moreover, there exist isomorphisms
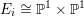 $E_{i}\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
such that
$E_{i}\cong \mathbb{P}^{1}\times \mathbb{P}^{1}$
such that
![]() $\imath$
acts by interchanging the two factors. Thus the quotient
$\imath$
acts by interchanging the two factors. Thus the quotient
![]() ${\mathcal{X}}_{2}^{\prime }/\imath$
is a model of
${\mathcal{X}}_{2}^{\prime }/\imath$
is a model of
![]() $Y$
over
$Y$
over
![]() $\mathbb{Z}_{p}$
, whose special fiber is a rational surface
$\mathbb{Z}_{p}$
, whose special fiber is a rational surface
![]() $X_{p}^{\prime }/\imath$
(a so-called Coble surface) meeting transversally four
$X_{p}^{\prime }/\imath$
(a so-called Coble surface) meeting transversally four
![]() $\mathbb{P}^{2}$
’s, that is, a semi-stable degeneration of flower pot type (see, [Reference PerssonPer77, §3.3]).
$\mathbb{P}^{2}$
’s, that is, a semi-stable degeneration of flower pot type (see, [Reference PerssonPer77, §3.3]).
Seeking a contradiction, we assume that
![]() $Y$
has potential good reduction. Then there exists a finite extension
$Y$
has potential good reduction. Then there exists a finite extension
![]() $L/\mathbb{Q}_{p}$
and a smooth model
$L/\mathbb{Q}_{p}$
and a smooth model
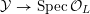 ${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
${\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
![]() $Y_{L}$
. Let
$Y_{L}$
. Let
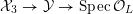 ${\mathcal{X}}_{3}\rightarrow {\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
be its K3 double cover, which is a family of smooth K3 surfaces with generic fiber
${\mathcal{X}}_{3}\rightarrow {\mathcal{Y}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
be its K3 double cover, which is a family of smooth K3 surfaces with generic fiber
![]() $X_{L}$
, whose fixed point free involution specializes to a fixed point free involution in the special fiber of
$X_{L}$
, whose fixed point free involution specializes to a fixed point free involution in the special fiber of
![]() ${\mathcal{X}}_{3}$
.
${\mathcal{X}}_{3}$
.
Now,
![]() ${\mathcal{X}}_{3}$
and the base-change of
${\mathcal{X}}_{3}$
and the base-change of
![]() ${\mathcal{X}}_{1}^{\prime }$
to
${\mathcal{X}}_{1}^{\prime }$
to
![]() ${\mathcal{O}}_{L}$
both are smooth models of
${\mathcal{O}}_{L}$
both are smooth models of
![]() $X_{L}$
. The isomorphism of generic fibers extends to a birational map of special fibers. The involution on generic fibers extends to rational involutions of the two special fibers, compatible with the just established birational map. Since both special fibers are K3 surfaces, the birational maps and rational involutions extend to isomorphisms and involutions. However, in one special fiber the involution acts without fixed points, whereas it has four fixed curves in the other, which contradicts the assumption. ◻
$X_{L}$
. The isomorphism of generic fibers extends to a birational map of special fibers. The involution on generic fibers extends to rational involutions of the two special fibers, compatible with the just established birational map. Since both special fibers are K3 surfaces, the birational maps and rational involutions extend to isomorphisms and involutions. However, in one special fiber the involution acts without fixed points, whereas it has four fixed curves in the other, which contradicts the assumption. ◻
4 Existence and termination of flops
Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial canonical sheaf and assume that we have a smooth model
$K$
with numerically trivial canonical sheaf and assume that we have a smooth model
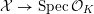 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Now, if
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Now, if
![]() ${\mathcal{L}}$
is an ample invertible sheaf on
${\mathcal{L}}$
is an ample invertible sheaf on
![]() $X$
, then its specialization
$X$
, then its specialization
![]() ${\mathcal{L}}_{0}$
to the special fiber may not be ample, and not even be nef. In this section, we show that there exists a finite sequence of birational modifications (flops) of
${\mathcal{L}}_{0}$
to the special fiber may not be ample, and not even be nef. In this section, we show that there exists a finite sequence of birational modifications (flops) of
![]() ${\mathcal{X}}$
, such that we eventually arrive at a smooth model
${\mathcal{X}}$
, such that we eventually arrive at a smooth model
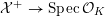 ${\mathcal{X}}^{+}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
of
${\mathcal{X}}^{+}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
of
![]() $X$
, such that the restriction of
$X$
, such that the restriction of
![]() ${\mathcal{L}}$
to the special fiber of
${\mathcal{L}}$
to the special fiber of
![]() ${\mathcal{X}}^{+}$
is big and nef. We end this section by showing that any two smooth models of
${\mathcal{X}}^{+}$
is big and nef. We end this section by showing that any two smooth models of
![]() $X$
over
$X$
over
![]() ${\mathcal{O}}_{K}$
are related by a finite sequence of flopping contractions and their inverses.
${\mathcal{O}}_{K}$
are related by a finite sequence of flopping contractions and their inverses.
We start by adjusting [Reference Kollár and MoriKM98, Definition 3.33] and [Reference Kollár and MoriKM98, Definition 6.10] to our situation.
Definition 4.1. Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
that admits a smooth model
$\unicode[STIX]{x1D714}_{X/K}$
that admits a smooth model
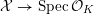 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Then we have the following.
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Then we have the following.
-
(i) A proper and birational morphism
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
over
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
over
 ${\mathcal{O}}_{K}$
is called a flopping contraction if
${\mathcal{O}}_{K}$
is called a flopping contraction if
 ${\mathcal{Y}}$
is normal and if the exceptional locus of
${\mathcal{Y}}$
is normal and if the exceptional locus of
 $f$
is of codimension at least two.
$f$
is of codimension at least two. -
(ii) If
 $D$
is a Cartier divisor on
$D$
is a Cartier divisor on
 ${\mathcal{X}}$
, then a birational map
${\mathcal{X}}$
, then a birational map
 ${\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
over
${\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
over
 ${\mathcal{O}}_{K}$
is called a
${\mathcal{O}}_{K}$
is called a
 $D$
-flop if it decomposes into a flopping contraction
$D$
-flop if it decomposes into a flopping contraction
 $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
followed by (the inverse of) a flopping contraction
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
followed by (the inverse of) a flopping contraction
 $f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{Y}}$
such that
$f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{Y}}$
such that
 $-D$
is
$-D$
is
 $f$
-ample and
$f$
-ample and
 $D^{+}$
is
$D^{+}$
is
 $f^{+}$
-ample, where
$f^{+}$
-ample, where
 $D^{+}$
denotes the strict transform of
$D^{+}$
denotes the strict transform of
 $D$
on
$D$
on
 ${\mathcal{X}}^{+}$
. If
${\mathcal{X}}^{+}$
. If
 ${\mathcal{L}}$
is an invertible sheaf on
${\mathcal{L}}$
is an invertible sheaf on
 ${\mathcal{X}}$
, we similarly define an
${\mathcal{X}}$
, we similarly define an
 ${\mathcal{L}}$
-flop.
${\mathcal{L}}$
-flop. -
(iii) A morphism
 $f^{+}$
as in (2) is also called a flop of
$f^{+}$
as in (2) is also called a flop of
 $f$
.
$f$
.
In general, one also has to assume that
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{K}}$
is numerically
$\unicode[STIX]{x1D714}_{{\mathcal{X}}/{\mathcal{O}}_{K}}$
is numerically
![]() $f$
-trivial in the definition of a flopping contraction. However, in our situation this is automatic. Also, a flop of
$f$
-trivial in the definition of a flopping contraction. However, in our situation this is automatic. Also, a flop of
![]() $f$
, if it exists, does not depend on the choice of
$f$
, if it exists, does not depend on the choice of
![]() $D$
by [Reference Kollár and MoriKM98, Corollary 6.4] and [Reference Kollár and MoriKM98, Definition 6.10]. This justifies talking about flops without referring to the divisor
$D$
by [Reference Kollár and MoriKM98, Corollary 6.4] and [Reference Kollár and MoriKM98, Definition 6.10]. This justifies talking about flops without referring to the divisor
![]() $D$
.
$D$
.
4.1 Existence of flops
The following is an adaptation of Kollár’s proof [Reference KollárKol89, Proposition 2.2] of the existence of
![]() $3$
-fold flops over
$3$
-fold flops over
![]() $\mathbb{C}$
to our situation, which deals with special flops in mixed characteristic.
$\mathbb{C}$
to our situation, which deals with special flops in mixed characteristic.
Proposition 4.2 (Existence of flops).
Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
that has a smooth model
$\unicode[STIX]{x1D714}_{X/K}$
that has a smooth model
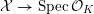 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. If
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. If
![]() ${\mathcal{L}}$
is an ample invertible sheaf on
${\mathcal{L}}$
is an ample invertible sheaf on
![]() $X$
and
$X$
and
![]() $C$
is an integral (but not necessarily geometrically integral) curve on the special fiber
$C$
is an integral (but not necessarily geometrically integral) curve on the special fiber
![]() ${\mathcal{X}}_{0}$
with
${\mathcal{X}}_{0}$
with
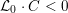 ${\mathcal{L}}_{0}\cdot C<0$
, then there exists a flopping contraction
${\mathcal{L}}_{0}\cdot C<0$
, then there exists a flopping contraction
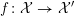 $f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
and its
$f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
and its
![]() ${\mathcal{L}}$
-flop
${\mathcal{L}}$
-flop
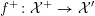 $f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{X}}^{\prime }$
with the following properties:
$f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{X}}^{\prime }$
with the following properties:
-
(i)
 $f$
contracts
$f$
contracts
 $C$
and no other curves;
$C$
and no other curves; -
(ii)
 ${\mathcal{X}}^{+}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
is a smooth model of
${\mathcal{X}}^{+}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
is a smooth model of
 $X$
;
$X$
; -
(iii)
 $f$
and
$f$
and
 $f^{+}$
induce isomorphisms of generic fibers;
$f^{+}$
induce isomorphisms of generic fibers; -
(iv)
 ${\mathcal{L}}_{0}^{+}\cdot C^{+}>0$
, where
${\mathcal{L}}_{0}^{+}\cdot C^{+}>0$
, where
 ${\mathcal{L}}^{+}$
denotes the extension of
${\mathcal{L}}^{+}$
denotes the extension of
 ${\mathcal{L}}$
on
${\mathcal{L}}$
on
 ${\mathcal{X}}^{+}$
, and where
${\mathcal{X}}^{+}$
, and where
 $C^{+}$
denotes the flopped curve (that is, the exceptional locus of
$C^{+}$
denotes the flopped curve (that is, the exceptional locus of
 $f^{+}$
).
$f^{+}$
).
Proof. Since
![]() ${\mathcal{L}}$
is ample,
${\mathcal{L}}$
is ample,
![]() ${\mathcal{L}}^{\otimes n}$
is effective for
${\mathcal{L}}^{\otimes n}$
is effective for
![]() $n\gg 0$
, and thus also its specialization
$n\gg 0$
, and thus also its specialization
![]() ${\mathcal{L}}_{0}^{\otimes n}$
to the special fiber
${\mathcal{L}}_{0}^{\otimes n}$
to the special fiber
![]() ${\mathcal{X}}_{0}$
is effective. In particular,
${\mathcal{X}}_{0}$
is effective. In particular,
![]() ${\mathcal{L}}_{0}$
has positive intersection with every ample divisor on
${\mathcal{L}}_{0}$
has positive intersection with every ample divisor on
![]() ${\mathcal{X}}_{0}$
, that is,
${\mathcal{X}}_{0}$
, that is,
![]() ${\mathcal{L}}_{0}$
is pseudo-effective. Thus there exists a Zariski–Fujita decomposition on
${\mathcal{L}}_{0}$
is pseudo-effective. Thus there exists a Zariski–Fujita decomposition on
![]() $({\mathcal{X}}_{0})_{\overline{k}}$
$({\mathcal{X}}_{0})_{\overline{k}}$
 $$\begin{eqnarray}({\mathcal{L}}_{0})_{\overline{k}}=P+N,\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{L}}_{0})_{\overline{k}}=P+N,\end{eqnarray}$$
where
![]() $P$
is nef, and where
$P$
is nef, and where
![]() $N$
is a sum of effective divisors, whose intersection matrix is negative definite; see, for example, [Reference BădescuBăd01, Theorem 14.14]. Since
$N$
is a sum of effective divisors, whose intersection matrix is negative definite; see, for example, [Reference BădescuBăd01, Theorem 14.14]. Since
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial, the adjunction formula shows that every reduced and irreducible curve in
$\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial, the adjunction formula shows that every reduced and irreducible curve in
![]() $N$
is a
$N$
is a
![]() $\mathbb{P}^{1}$
with self-intersection
$\mathbb{P}^{1}$
with self-intersection
![]() $-2$
, that is, a
$-2$
, that is, a
![]() $(-2)$
-curve. Moreover, negative definiteness and the classification of Cartan matrices implies that
$(-2)$
-curve. Moreover, negative definiteness and the classification of Cartan matrices implies that
![]() $N$
is a disjoint union of ADE curves. Next,
$N$
is a disjoint union of ADE curves. Next,
![]() $k$
is perfect and since the Zariski–Fujita decomposition is unique, it is stable under
$k$
is perfect and since the Zariski–Fujita decomposition is unique, it is stable under
![]() $G_{k}$
, and thus descends to
$G_{k}$
, and thus descends to
![]() ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
After these preparations, let
![]() $C$
be as in the statement, that is,
$C$
be as in the statement, that is,
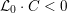 ${\mathcal{L}}_{0}\cdot C<0$
. First, we want to show that there exists a morphism
${\mathcal{L}}_{0}\cdot C<0$
. First, we want to show that there exists a morphism
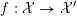 $f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
of algebraic spaces that contracts
$f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
of algebraic spaces that contracts
![]() $C$
. Being contained in the support of
$C$
. Being contained in the support of
![]() $N$
, the base-change
$N$
, the base-change
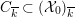 $C_{\overline{k}}\subset ({\mathcal{X}}_{0})_{\overline{k}}$
is a disjoint union of ADE curves. Since
$C_{\overline{k}}\subset ({\mathcal{X}}_{0})_{\overline{k}}$
is a disjoint union of ADE curves. Since
![]() $C^{2}<0$
, Artin showed that there exists a morphism of projective surfaces over
$C^{2}<0$
, Artin showed that there exists a morphism of projective surfaces over
![]() $k$
$k$
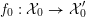 $$\begin{eqnarray}f_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}f_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }\end{eqnarray}$$
that contracts
![]() $C$
and nothing else (see [Reference BădescuBăd01, Theorem 3.9], for example). Since
$C$
and nothing else (see [Reference BădescuBăd01, Theorem 3.9], for example). Since
![]() $C_{\overline{k}}$
is a union of ADE-curves, it follows that
$C_{\overline{k}}$
is a union of ADE-curves, it follows that
![]() $({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has RDP singularities, which are rational and Gorenstein. Thus also
$({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has RDP singularities, which are rational and Gorenstein. Thus also
![]() ${\mathcal{X}}_{0}^{\prime }$
has rational Gorenstein singularities.
${\mathcal{X}}_{0}^{\prime }$
has rational Gorenstein singularities.
For all
![]() $n\geqslant 0$
, we define
$n\geqslant 0$
, we define
 $$\begin{eqnarray}{\mathcal{X}}_{n}:={\mathcal{X}}\times _{\operatorname{Spec}{\mathcal{O}}_{K}}\operatorname{Spec}({\mathcal{O}}_{K}/\mathfrak{m}^{n+1}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}_{n}:={\mathcal{X}}\times _{\operatorname{Spec}{\mathcal{O}}_{K}}\operatorname{Spec}({\mathcal{O}}_{K}/\mathfrak{m}^{n+1}).\end{eqnarray}$$
Since
![]() $f_{0}$
is a contraction with
$f_{0}$
is a contraction with
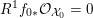 $R^{1}f_{0\ast }{\mathcal{O}}_{{\mathcal{X}}_{0}}=0$
, there exists a blow-down
$R^{1}f_{0\ast }{\mathcal{O}}_{{\mathcal{X}}_{0}}=0$
, there exists a blow-down
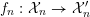 $f_{n}:{\mathcal{X}}_{n}\rightarrow {\mathcal{X}}_{n}^{\prime }$
that extends
$f_{n}:{\mathcal{X}}_{n}\rightarrow {\mathcal{X}}_{n}^{\prime }$
that extends
![]() $f_{0}$
, see [Reference Cynk and van StratenCvS09, Theorem 3.1]. Passing to limits, we obtain a contraction of formal schemes
$f_{0}$
, see [Reference Cynk and van StratenCvS09, Theorem 3.1]. Passing to limits, we obtain a contraction of formal schemes
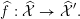 $$\begin{eqnarray}\widehat{f}:\widehat{{\mathcal{X}}}\rightarrow \widehat{{\mathcal{X}}}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{f}:\widehat{{\mathcal{X}}}\rightarrow \widehat{{\mathcal{X}}}^{\prime }.\end{eqnarray}$$
By [Reference ArtinArt70, Theorem 3.1], there exists a contraction of algebraic spaces
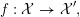 $$\begin{eqnarray}f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}f:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime },\end{eqnarray}$$
whose completion along their special fibers coincides with
![]() $\widehat{f}$
. In particular,
$\widehat{f}$
. In particular,
![]() $f$
is an isomorphism outside
$f$
is an isomorphism outside
![]() $C$
and contracts
$C$
and contracts
![]() $C$
to a singular point
$C$
to a singular point
![]() $w\in {\mathcal{X}}^{\prime }$
.
$w\in {\mathcal{X}}^{\prime }$
.
Let
![]() $\widehat{w}$
be the formal completion of
$\widehat{w}$
be the formal completion of
![]() ${\mathcal{X}}^{\prime }$
along
${\mathcal{X}}^{\prime }$
along
![]() $w$
, and let
$w$
, and let
be the formal fiber over
![]() $\widehat{f}$
. Then
$\widehat{f}$
. Then
![]() $\widehat{w}$
is a formal affine scheme, say
$\widehat{w}$
is a formal affine scheme, say
![]() $\operatorname{Spf}R$
, and let
$\operatorname{Spf}R$
, and let
![]() $k^{\prime }$
be the residue field, which is a finite extension of
$k^{\prime }$
be the residue field, which is a finite extension of
![]() $k$
. Let
$k$
. Let
![]() ${\mathcal{O}}_{K^{\prime }}$
be the unramified extension of
${\mathcal{O}}_{K^{\prime }}$
be the unramified extension of
![]() ${\mathcal{O}}_{K}$
corresponding to the field extension
${\mathcal{O}}_{K}$
corresponding to the field extension
![]() $k\subseteq k^{\prime }$
. Since
$k\subseteq k^{\prime }$
. Since
![]() $k\subseteq k^{\prime }$
is separable,
$k\subseteq k^{\prime }$
is separable,
![]() $k^{\prime }$
arises by adjoining a root
$k^{\prime }$
arises by adjoining a root
![]() $\unicode[STIX]{x1D6FC}$
of some monic polynomial
$\unicode[STIX]{x1D6FC}$
of some monic polynomial
![]() $f$
with values
$f$
with values
![]() $k$
. After lifting
$k$
. After lifting
![]() $f$
to a polynomial with values in
$f$
to a polynomial with values in
![]() ${\mathcal{O}}_{K}$
, and using that
${\mathcal{O}}_{K}$
, and using that
![]() $R$
is Henselian, we can lift
$R$
is Henselian, we can lift
![]() $\unicode[STIX]{x1D6FC}$
to
$\unicode[STIX]{x1D6FC}$
to
![]() $R$
, which shows that
$R$
, which shows that
![]() ${\mathcal{O}}_{K^{\prime }}$
is contained in
${\mathcal{O}}_{K^{\prime }}$
is contained in
![]() $R$
. In particular, we can view
$R$
. In particular, we can view
![]() $R$
as a local
$R$
as a local
![]() ${\mathcal{O}}_{K^{\prime }}$
-algebra without residue field extension – we denote by
${\mathcal{O}}_{K^{\prime }}$
-algebra without residue field extension – we denote by
![]() $\tilde{R}$
the ring
$\tilde{R}$
the ring
![]() $R$
considered as
$R$
considered as
![]() ${\mathcal{O}}_{K^{\prime }}$
-algebra.
${\mathcal{O}}_{K^{\prime }}$
-algebra.
Then the special fiber of
![]() $\operatorname{Spf}\tilde{R}$
is a rational singularity of multiplicity
$\operatorname{Spf}\tilde{R}$
is a rational singularity of multiplicity
![]() $2$
, and thus, by [Reference LipmanLip69, Lemma 23.4], the completion of the local ring of the special fiber is of the form
$2$
, and thus, by [Reference LipmanLip69, Lemma 23.4], the completion of the local ring of the special fiber is of the form
 $$\begin{eqnarray}k^{\prime }[[x,y,z]]/(h^{\prime }(x,y,z)).\end{eqnarray}$$
$$\begin{eqnarray}k^{\prime }[[x,y,z]]/(h^{\prime }(x,y,z)).\end{eqnarray}$$
Using Hensel’s lemma, we may assume after a change of coordinates that the power series
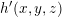 $h^{\prime }(x,y,z)$
is of the form
$h^{\prime }(x,y,z)$
is of the form
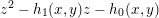 $z^{2}-h_{1}(x,y)z-h_{0}(x,y)$
for some polynomials
$z^{2}-h_{1}(x,y)z-h_{0}(x,y)$
for some polynomials
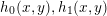 $h_{0}(x,y),h_{1}(x,y)$
. Using Hensel’s lemma again, the completion of
$h_{0}(x,y),h_{1}(x,y)$
. Using Hensel’s lemma again, the completion of
![]() $\tilde{R}$
is of the form
$\tilde{R}$
is of the form
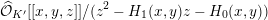 $$\begin{eqnarray}\widehat{{\mathcal{O}}}_{K^{\prime }}[[x,y,z]]/(z^{2}-H_{1}(x,y)z-H_{0}(x,y))\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{O}}}_{K^{\prime }}[[x,y,z]]/(z^{2}-H_{1}(x,y)z-H_{0}(x,y))\end{eqnarray}$$
where
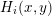 $H_{i}(x,y)$
is congruent to
$H_{i}(x,y)$
is congruent to
![]() $h_{i}(x,y)$
modulo the maximal ideal of
$h_{i}(x,y)$
modulo the maximal ideal of
![]() $\widehat{{\mathcal{O}}}_{K^{\prime }}$
for
$\widehat{{\mathcal{O}}}_{K^{\prime }}$
for
![]() $i=1,2$
; see also [Reference KawamataKaw94, Theorem 4.4]. (If
$i=1,2$
; see also [Reference KawamataKaw94, Theorem 4.4]. (If
![]() $p\neq 2$
, we may even assume
$p\neq 2$
, we may even assume
![]() $h_{1}=0$
and
$h_{1}=0$
and
![]() $H_{1}=0$
.) We denote by
$H_{1}=0$
.) We denote by
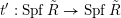 $t^{\prime }:\operatorname{Spf}\tilde{R}\rightarrow \operatorname{Spf}\tilde{R}$
the involution induced by
$t^{\prime }:\operatorname{Spf}\tilde{R}\rightarrow \operatorname{Spf}\tilde{R}$
the involution induced by
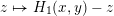 $z\mapsto H_{1}(x,y)-z$
. It is not difficult to see that
$z\mapsto H_{1}(x,y)-z$
. It is not difficult to see that
![]() $t^{\prime }$
induces
$t^{\prime }$
induces
![]() $-\!\operatorname{id}$
on local Picard groups, see, for example, [Reference KollárKol89, Example 2.3]. Since
$-\!\operatorname{id}$
on local Picard groups, see, for example, [Reference KollárKol89, Example 2.3]. Since
![]() $R$
is equal to
$R$
is equal to
![]() $\tilde{R}$
considered as rings, we have established an involution
$\tilde{R}$
considered as rings, we have established an involution
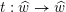 $t:\widehat{w}\rightarrow \widehat{w}$
that induces
$t:\widehat{w}\rightarrow \widehat{w}$
that induces
![]() $-\text{id}$
on local Picard groups. We denote by
$-\text{id}$
on local Picard groups. We denote by
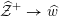 $$\begin{eqnarray}\widehat{{\mathcal{Z}}}^{+}\rightarrow \widehat{w}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{Z}}}^{+}\rightarrow \widehat{w}\end{eqnarray}$$
the composition
![]() $t\circ \widehat{f}$
. By [Reference KollárKol89, Proposition 2.2], this gives the desired flop formally.
$t\circ \widehat{f}$
. By [Reference KollárKol89, Proposition 2.2], this gives the desired flop formally.
By [Reference ArtinArt70, Theorem 3.2], there exists a dilatation
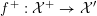 $f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{X}}^{\prime }$
of algebraic spaces, such that the formal completion of
$f^{+}:{\mathcal{X}}^{+}\rightarrow {\mathcal{X}}^{\prime }$
of algebraic spaces, such that the formal completion of
![]() ${\mathcal{X}}^{+}$
along the exceptional locus of
${\mathcal{X}}^{+}$
along the exceptional locus of
![]() $f^{+}$
is given by the just-constructed
$f^{+}$
is given by the just-constructed
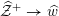 $\widehat{{\mathcal{Z}}}^{+}\rightarrow \widehat{w}$
. Thus there exists a birational and rational map
$\widehat{{\mathcal{Z}}}^{+}\rightarrow \widehat{w}$
. Thus there exists a birational and rational map
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+},\end{eqnarray}$$
which is an isomorphism outside
![]() $C$
. From the glueing construction it is clear that
$C$
. From the glueing construction it is clear that
![]() ${\mathcal{X}}^{+}$
is a smooth model of
${\mathcal{X}}^{+}$
is a smooth model of
![]() $X$
over
$X$
over
![]() ${\mathcal{O}}_{K}$
. Finally, from the formal picture above, it is clear that the restriction of
${\mathcal{O}}_{K}$
. Finally, from the formal picture above, it is clear that the restriction of
![]() ${\mathcal{L}}^{+}$
to
${\mathcal{L}}^{+}$
to
![]() ${\mathcal{X}}_{0}^{+}$
has positive intersection with the flopped curve
${\mathcal{X}}_{0}^{+}$
has positive intersection with the flopped curve
![]() $C^{+}$
.◻
$C^{+}$
.◻
4.2 Termination of flops
Having established the existence of certain flops in mixed characteristic, we now show that there is no infinite sequence of them. To do so, one can adjust the proof of termination of flops from [Reference Kollár and MoriKM98, Theorem 6.17 and Corollary 6.19] over
![]() $\mathbb{C}$
to our situation. Instead, we give another argument that was kindly suggested to us by the referee.
$\mathbb{C}$
to our situation. Instead, we give another argument that was kindly suggested to us by the referee.
We keep the notation and assumptions of Proposition 4.2. Then there are two isomorphisms between the
![]() $\ell$
-adic cohomology groups of the special fibers
$\ell$
-adic cohomology groups of the special fibers
![]() ${\mathcal{X}}_{0}$
and
${\mathcal{X}}_{0}$
and
![]() ${\mathcal{X}}_{0}^{+}$
.
${\mathcal{X}}_{0}^{+}$
.
-
(i) The first is by composing the comparison isomorphisms relating the cohomology groups of special and generic fibers of
 ${\mathcal{X}}$
and
${\mathcal{X}}$
and
 ${\mathcal{X}}^{+}$
${\mathcal{X}}^{+}$
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0}^{+})_{\overline{k}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0}^{+})_{\overline{k}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
-
(ii) Next, the composition
 $\unicode[STIX]{x1D711}:=(f^{+})^{-1}\circ f:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
induces a birational and rational map of special fibers
$\unicode[STIX]{x1D711}:=(f^{+})^{-1}\circ f:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
induces a birational and rational map of special fibers
 $\unicode[STIX]{x1D711}_{0}:{\mathcal{X}}_{0}{\dashrightarrow}{\mathcal{X}}_{0}^{+}$
, which extends to an isomorphism, since
$\unicode[STIX]{x1D711}_{0}:{\mathcal{X}}_{0}{\dashrightarrow}{\mathcal{X}}_{0}^{+}$
, which extends to an isomorphism, since
 ${\mathcal{X}}_{0}$
and
${\mathcal{X}}_{0}$
and
 ${\mathcal{X}}_{0}^{+}$
are minimal surfaces of Kodaira dimension at least
${\mathcal{X}}_{0}^{+}$
are minimal surfaces of Kodaira dimension at least
 $0$
. Thus we obtain a second isomorphism via pull-back
$0$
. Thus we obtain a second isomorphism via pull-back  $$\begin{eqnarray}\unicode[STIX]{x1D711}_{0}^{\ast }:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0}^{+})_{\overline{k}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{0}^{\ast }:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0}^{+})_{\overline{k}},\mathbb{Q}_{\ell })(1)\cong H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1).\end{eqnarray}$$
We note that both isomorphisms respect the intersection product coming from Poincaré duality, that is, they are isometries. For a
![]() $(-2)$
-curve
$(-2)$
-curve
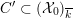 $C^{\prime }\subset ({\mathcal{X}}_{0})_{\overline{k}}$
, we let
$C^{\prime }\subset ({\mathcal{X}}_{0})_{\overline{k}}$
, we let
![]() $[C^{\prime }]$
be the associated cycle class in
$[C^{\prime }]$
be the associated cycle class in
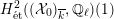 $H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)$
and we define the reflection in
$H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)$
and we define the reflection in
![]() $C^{\prime }$
to be the isometry
$C^{\prime }$
to be the isometry
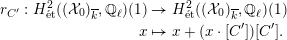 $$\begin{eqnarray}\displaystyle r_{C^{\prime }}:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1) & \rightarrow & \displaystyle H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)\nonumber\\ \displaystyle x & \mapsto & \displaystyle x+(x\cdot [C^{\prime }])[C^{\prime }].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{C^{\prime }}:H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1) & \rightarrow & \displaystyle H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)\nonumber\\ \displaystyle x & \mapsto & \displaystyle x+(x\cdot [C^{\prime }])[C^{\prime }].\nonumber\end{eqnarray}$$
The following lemma compares the isometries
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D711}_{0}^{\ast }$
in terms of reflections in
$\unicode[STIX]{x1D711}_{0}^{\ast }$
in terms of reflections in
![]() $(-2)$
-curves.
$(-2)$
-curves.
Lemma 4.3. We keep the notation and assumptions as in Proposition 4.2 and denote by
 $C_{1},\ldots ,C_{m}$
the connected components of
$C_{1},\ldots ,C_{m}$
the connected components of
![]() $C_{\overline{k}}$
. Then
$C_{\overline{k}}$
. Then
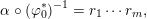 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}_{0}^{\ast })^{-1}=r_{1}\cdots r_{m},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}_{0}^{\ast })^{-1}=r_{1}\cdots r_{m},\end{eqnarray}$$
where either:
-
(i) the connected components
 $C_{i}$
are disjoint
$C_{i}$
are disjoint
 $(-2)$
-curves and
$(-2)$
-curves and
 $r_{i}=r_{C_{i}}$
; or
$r_{i}=r_{C_{i}}$
; or -
(ii) each
 $C_{i}$
is the union of two
$C_{i}$
is the union of two
 $(-2)$
-curves
$(-2)$
-curves
 $C_{i,1}$
and
$C_{i,1}$
and
 $C_{i,2}$
intersecting in one point and
$C_{i,2}$
intersecting in one point and
 $r_{i}=r_{C_{i,1}}r_{C_{i,2}}r_{C_{i,1}}=r_{C_{i,2}}r_{C_{i,1}}r_{C_{i,2}}$
.
$r_{i}=r_{C_{i,1}}r_{C_{i,2}}r_{C_{i,1}}=r_{C_{i,2}}r_{C_{i,1}}r_{C_{i,2}}$
.
Proof. First, we consider the case, where
![]() $C$
is geometrically integral. Let
$C$
is geometrically integral. Let
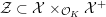 ${\mathcal{Z}}\subset {\mathcal{X}}\times _{{\mathcal{O}}_{K}}{\mathcal{X}}^{+}$
be the closure of the diagonal
${\mathcal{Z}}\subset {\mathcal{X}}\times _{{\mathcal{O}}_{K}}{\mathcal{X}}^{+}$
be the closure of the diagonal
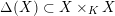 $\unicode[STIX]{x1D6E5}(X)\subset X\times _{K}X$
. Then it is not difficult to see that the isomorphism
$\unicode[STIX]{x1D6E5}(X)\subset X\times _{K}X$
. Then it is not difficult to see that the isomorphism
![]() $\unicode[STIX]{x1D6FC}$
is given by
$\unicode[STIX]{x1D6FC}$
is given by
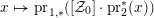 $x\mapsto \operatorname{pr}_{1,\ast }([{\mathcal{Z}}_{0}]\cdot \operatorname{pr}_{2}^{\ast }(x))$
(see also Lemma 5.6 below). We set
$x\mapsto \operatorname{pr}_{1,\ast }([{\mathcal{Z}}_{0}]\cdot \operatorname{pr}_{2}^{\ast }(x))$
(see also Lemma 5.6 below). We set
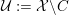 ${\mathcal{U}}:={\mathcal{X}}\setminus C$
and
${\mathcal{U}}:={\mathcal{X}}\setminus C$
and
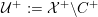 ${\mathcal{U}}^{+}:={\mathcal{X}}^{+}\setminus C^{+}$
. Then we have a commutative diagram with exact rows
${\mathcal{U}}^{+}:={\mathcal{X}}^{+}\setminus C^{+}$
. Then we have a commutative diagram with exact rows
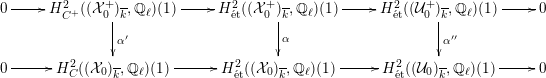
where
![]() $\unicode[STIX]{x1D6FC}^{\prime \prime }$
is also defined by
$\unicode[STIX]{x1D6FC}^{\prime \prime }$
is also defined by
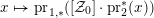 $x\mapsto \operatorname{pr}_{1,\ast }([{\mathcal{Z}}_{0}]\cdot \operatorname{pr}_{2}^{\ast }(x))$
and where
$x\mapsto \operatorname{pr}_{1,\ast }([{\mathcal{Z}}_{0}]\cdot \operatorname{pr}_{2}^{\ast }(x))$
and where
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is the map induced by
$\unicode[STIX]{x1D6FC}^{\prime }$
is the map induced by
![]() $\unicode[STIX]{x1D6FC}$
. By purity, the left terms are one-dimensional and generated by the classes
$\unicode[STIX]{x1D6FC}$
. By purity, the left terms are one-dimensional and generated by the classes
![]() $[C]$
and
$[C]$
and
![]() $[C^{+}]$
, respectively. Moreover, the right terms are canonically isomorphic to the orthogonal complements of the left terms. Since
$[C^{+}]$
, respectively. Moreover, the right terms are canonically isomorphic to the orthogonal complements of the left terms. Since
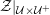 ${\mathcal{Z}}|_{{\mathcal{U}}\times {\mathcal{U}}^{+}}$
is the graph of the isomorphism
${\mathcal{Z}}|_{{\mathcal{U}}\times {\mathcal{U}}^{+}}$
is the graph of the isomorphism
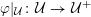 $\unicode[STIX]{x1D711}|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{U}}^{+}$
, it follows that
$\unicode[STIX]{x1D711}|_{{\mathcal{U}}}:{\mathcal{U}}\rightarrow {\mathcal{U}}^{+}$
, it follows that
![]() $\unicode[STIX]{x1D6FC}^{\prime \prime }$
coincides with the pull-back by the isomorphism
$\unicode[STIX]{x1D6FC}^{\prime \prime }$
coincides with the pull-back by the isomorphism
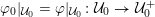 $\unicode[STIX]{x1D711}_{0}|_{{\mathcal{U}}_{0}}=\unicode[STIX]{x1D711}|_{{\mathcal{U}}_{0}}:{\mathcal{U}}_{0}\rightarrow {\mathcal{U}}_{0}^{+}$
. Since
$\unicode[STIX]{x1D711}_{0}|_{{\mathcal{U}}_{0}}=\unicode[STIX]{x1D711}|_{{\mathcal{U}}_{0}}:{\mathcal{U}}_{0}\rightarrow {\mathcal{U}}_{0}^{+}$
. Since
![]() $\unicode[STIX]{x1D6FC}$
is an isometry, so is
$\unicode[STIX]{x1D6FC}$
is an isometry, so is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
, and it maps
$\unicode[STIX]{x1D6FC}^{\prime }$
, and it maps
![]() $[C^{+}]$
either to
$[C^{+}]$
either to
![]() $[C]$
or to
$[C]$
or to
![]() $-[C]$
. From
$-[C]$
. From
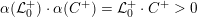 $\unicode[STIX]{x1D6FC}({\mathcal{L}}_{0}^{+})\cdot \unicode[STIX]{x1D6FC}(C^{+})={\mathcal{L}}_{0}^{+}\cdot C^{+}>0$
and
$\unicode[STIX]{x1D6FC}({\mathcal{L}}_{0}^{+})\cdot \unicode[STIX]{x1D6FC}(C^{+})={\mathcal{L}}_{0}^{+}\cdot C^{+}>0$
and
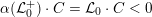 $\unicode[STIX]{x1D6FC}({\mathcal{L}}_{0}^{+})\cdot C={\mathcal{L}}_{0}\cdot C<0$
, we conclude
$\unicode[STIX]{x1D6FC}({\mathcal{L}}_{0}^{+})\cdot C={\mathcal{L}}_{0}\cdot C<0$
, we conclude
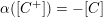 $\unicode[STIX]{x1D6FC}([C^{+}])=-[C]$
. Putting these observations together, we find
$\unicode[STIX]{x1D6FC}([C^{+}])=-[C]$
. Putting these observations together, we find
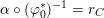 $\unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}_{0}^{\ast })^{-1}=r_{C}$
.
$\unicode[STIX]{x1D6FC}\circ (\unicode[STIX]{x1D711}_{0}^{\ast })^{-1}=r_{C}$
.
Now, we consider the general case. Since the absolute Galois group
![]() $G_{k}$
acts transitively on the
$G_{k}$
acts transitively on the
![]() $m$
connected components, they are mutually isomorphic. Since the flops in the disjoint
$m$
connected components, they are mutually isomorphic. Since the flops in the disjoint
![]() $C_{i}$
commute, we may assume
$C_{i}$
commute, we may assume
![]() $m=1$
. As shown in the proof of Proposition 4.2,
$m=1$
. As shown in the proof of Proposition 4.2,
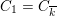 $C_{1}=C_{\overline{k}}$
is an ADE configuration of
$C_{1}=C_{\overline{k}}$
is an ADE configuration of
![]() $(-2)$
-curves. Since
$(-2)$
-curves. Since
![]() $G_{k}$
acts on the irreducible components of
$G_{k}$
acts on the irreducible components of
![]() $C_{i}$
transitively, it is not difficult to see from the classification of Dynkin diagrams that only configurations of type
$C_{i}$
transitively, it is not difficult to see from the classification of Dynkin diagrams that only configurations of type
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
can occur. We already treated the
$A_{2}$
can occur. We already treated the
![]() $A_{1}$
case above and thus we may assume an
$A_{1}$
case above and thus we may assume an
![]() $A_{2}$
-configuration, that is,
$A_{2}$
-configuration, that is,
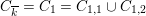 $C_{\overline{k}}=C_{1}=C_{1,1}\cup C_{1,2}$
. Passing to a finite unramified extension
$C_{\overline{k}}=C_{1}=C_{1,1}\cup C_{1,2}$
. Passing to a finite unramified extension
![]() $K^{\prime }/K$
corresponding to an extension
$K^{\prime }/K$
corresponding to an extension
![]() $k^{\prime }/k$
over which
$k^{\prime }/k$
over which
![]() $C$
splits, we consider the following diagram of flops and models over
$C$
splits, we consider the following diagram of flops and models over
![]() ${\mathcal{O}}_{K^{\prime }}$
:
${\mathcal{O}}_{K^{\prime }}$
:
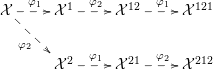
where
![]() $\unicode[STIX]{x1D711}_{j}$
denotes the flop at
$\unicode[STIX]{x1D711}_{j}$
denotes the flop at
![]() $C_{1,j}$
or at the corresponding curve on other models (note that our flops induce isomorphisms between the special fibers). A straightforward computation shows that
$C_{1,j}$
or at the corresponding curve on other models (note that our flops induce isomorphisms between the special fibers). A straightforward computation shows that
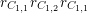 $r_{C_{1,1}}r_{C_{1,2}}r_{C_{1,1}}$
and
$r_{C_{1,1}}r_{C_{1,2}}r_{C_{1,1}}$
and
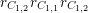 $r_{C_{1,2}}r_{C_{1,1}}r_{C_{1,2}}$
both act as
$r_{C_{1,2}}r_{C_{1,1}}r_{C_{1,2}}$
both act as
![]() $-\!\operatorname{id}$
on the one-dimensional subspace spanned by
$-\!\operatorname{id}$
on the one-dimensional subspace spanned by
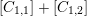 $[C_{1,1}]+[C_{1,2}]$
inside
$[C_{1,1}]+[C_{1,2}]$
inside
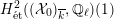 $H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)$
and as
$H_{\acute{\text{e}}\text{t}}^{2}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })(1)$
and as
![]() $\operatorname{id}$
on its orthogonal complement. Thus
$\operatorname{id}$
on its orthogonal complement. Thus
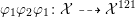 $\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{121}$
and
$\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{121}$
and
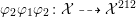 $\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{212}$
both satisfy the conditions of the flop of the contraction
$\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{212}$
both satisfy the conditions of the flop of the contraction
![]() $f$
. Hence, they coincide by the uniqueness of flops, and we set
$f$
. Hence, they coincide by the uniqueness of flops, and we set
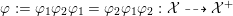 $\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
. Clearly,
$\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}:{\mathcal{X}}{\dashrightarrow}{\mathcal{X}}^{+}$
. Clearly,
![]() $\unicode[STIX]{x1D711}$
descends to
$\unicode[STIX]{x1D711}$
descends to
![]() ${\mathcal{O}}_{K}$
and coincides with the flop in
${\mathcal{O}}_{K}$
and coincides with the flop in
![]() $C$
established in Proposition 4.2.◻
$C$
established in Proposition 4.2.◻
We define a generalized
![]() $(-2)$
-curve on a smooth and proper surface
$(-2)$
-curve on a smooth and proper surface
![]() $X$
over a perfect field
$X$
over a perfect field
![]() $k$
to be an integral (but not necessarily geometrically integral) curve
$k$
to be an integral (but not necessarily geometrically integral) curve
![]() $C\subset X$
such that
$C\subset X$
such that
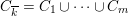 $C_{\overline{k}}=C_{1}\cup \cdots \cup C_{m}$
is a disjoint union of ADE curves of type
$C_{\overline{k}}=C_{1}\cup \cdots \cup C_{m}$
is a disjoint union of ADE curves of type
![]() $A_{1}$
or
$A_{1}$
or
![]() $A_{2}$
. We note that
$A_{2}$
. We note that
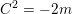 $C^{2}=-2m$
, that is, such curves are not necessarily of self-intersection
$C^{2}=-2m$
, that is, such curves are not necessarily of self-intersection
![]() $-2$
. Moreover, we define the reflection
$-2$
. Moreover, we define the reflection
![]() $r_{C}$
in
$r_{C}$
in
![]() $\operatorname{NS}(X)$
or
$\operatorname{NS}(X)$
or
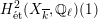 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{k}},\mathbb{Q}_{\ell })(1)$
to be equal to
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{k}},\mathbb{Q}_{\ell })(1)$
to be equal to
 $r_{1}\cdots r_{m}$
as in Lemma 4.3, which is equal to the map
$r_{1}\cdots r_{m}$
as in Lemma 4.3, which is equal to the map
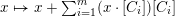 $x\mapsto x+\sum _{i=1}^{m}(x\cdot [C_{i}])[C_{i}]$
. The following lemma is essentially [Reference HuybrechtsHuy16, Remark 8.2.13].
$x\mapsto x+\sum _{i=1}^{m}(x\cdot [C_{i}])[C_{i}]$
. The following lemma is essentially [Reference HuybrechtsHuy16, Remark 8.2.13].
Lemma 4.4. Let
![]() $X$
be a smooth and projective surface over a perfect field with numerically trivial canonical sheaf, and let
$X$
be a smooth and projective surface over a perfect field with numerically trivial canonical sheaf, and let
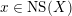 $x\in \operatorname{NS}(X)$
be a nonzero effective class with
$x\in \operatorname{NS}(X)$
be a nonzero effective class with
![]() $x^{2}\geqslant 0$
.
$x^{2}\geqslant 0$
.
-
(i) If
 $x$
is not nef, then there exists a generalized
$x$
is not nef, then there exists a generalized
 $(-2)$
-curve
$(-2)$
-curve
 $C$
with
$C$
with
 $C\cdot x<0$
and then
$C\cdot x<0$
and then
 $r_{C}(x)$
is non-zero and effective.
$r_{C}(x)$
is non-zero and effective. -
(ii) We define a sequence in
 $\operatorname{NS}(X)$
by setting
$\operatorname{NS}(X)$
by setting
 $x_{0}:=x$
and if
$x_{0}:=x$
and if
 $x_{i}$
is not nef, then we choose a generalized
$x_{i}$
is not nef, then we choose a generalized
 $(-2)$
-curve
$(-2)$
-curve
 $C^{i}$
with
$C^{i}$
with
 $C^{i}\cdot x_{i}<0$
and set
$C^{i}\cdot x_{i}<0$
and set
 $x_{i+1}:=r_{C^{i}}(x_{i})$
. Then
$x_{i+1}:=r_{C^{i}}(x_{i})$
. Then
 $\{x_{i}\}$
is a finite sequence of non-zero and effective classes in
$\{x_{i}\}$
is a finite sequence of non-zero and effective classes in
 $\operatorname{NS}(X)$
and the last class is nef.
$\operatorname{NS}(X)$
and the last class is nef.
Proof. Using the Zariski–Fujita decomposition of
![]() $x$
(see the proof of Proposition 4.2) and Lemma 4.3, we see that if
$x$
(see the proof of Proposition 4.2) and Lemma 4.3, we see that if
![]() $x$
is not nef, then a generalized
$x$
is not nef, then a generalized
![]() $(-2)$
-curve
$(-2)$
-curve
![]() $C$
with
$C$
with
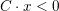 $C\cdot x<0$
indeed exists. Since Abelian and bielliptic surfaces do not admit smooth rational curves, we may assume that
$C\cdot x<0$
indeed exists. Since Abelian and bielliptic surfaces do not admit smooth rational curves, we may assume that
![]() $X$
is a K3 surface or an Enriques surface. Since
$X$
is a K3 surface or an Enriques surface. Since
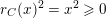 $r_{C}(x)^{2}=x^{2}\geqslant 0$
, it follows from the Riemann–Roch theorem that either
$r_{C}(x)^{2}=x^{2}\geqslant 0$
, it follows from the Riemann–Roch theorem that either
![]() $r_{C}(x)$
or
$r_{C}(x)$
or
![]() $-r_{C}(x)$
is effective. Let
$-r_{C}(x)$
is effective. Let
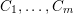 $C_{1},\ldots ,C_{m}$
be the connected components of
$C_{1},\ldots ,C_{m}$
be the connected components of
![]() $C_{\overline{k}}$
. Then we find
$C_{\overline{k}}$
. Then we find
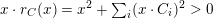 $x\cdot r_{C}(x)=x^{2}+\sum _{i}(x\cdot C_{i})^{2}>0$
, from which it follows that
$x\cdot r_{C}(x)=x^{2}+\sum _{i}(x\cdot C_{i})^{2}>0$
, from which it follows that
![]() $x$
and
$x$
and
![]() $r_{C}(x)$
belong to the same component of the cone
$r_{C}(x)$
belong to the same component of the cone
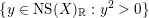 $\{y\in \operatorname{NS}(X)_{\mathbb{R}}:y^{2}>0\}$
, and thus
$\{y\in \operatorname{NS}(X)_{\mathbb{R}}:y^{2}>0\}$
, and thus
![]() $r_{C}(x)$
is effective. This establishes assertion (i).
$r_{C}(x)$
is effective. This establishes assertion (i).
To show assertion (ii), we fix an ample class
![]() $H$
of
$H$
of
![]() $X$
and let
$X$
and let
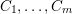 $C_{1},\ldots ,C_{m}$
be the connected components of
$C_{1},\ldots ,C_{m}$
be the connected components of
![]() $C_{\overline{k}}$
. Since
$C_{\overline{k}}$
. Since
![]() $G_{k}$
acts transitively on these components, we find
$G_{k}$
acts transitively on these components, we find
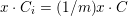 $x\cdot C_{i}=(1/m)x\cdot C$
and
$x\cdot C_{i}=(1/m)x\cdot C$
and
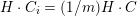 $H\cdot C_{i}=(1/m)H\cdot C$
, from which we conclude
$H\cdot C_{i}=(1/m)H\cdot C$
, from which we conclude
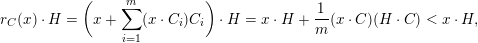 $$\begin{eqnarray}r_{C}(x)\cdot H=\biggl(x+\mathop{\sum }_{i=1}^{m}(x\cdot C_{i})C_{i}\biggr)\cdot H=x\cdot H+\frac{1}{m}(x\cdot C)(H\cdot C)<x\cdot H,\end{eqnarray}$$
$$\begin{eqnarray}r_{C}(x)\cdot H=\biggl(x+\mathop{\sum }_{i=1}^{m}(x\cdot C_{i})C_{i}\biggr)\cdot H=x\cdot H+\frac{1}{m}(x\cdot C)(H\cdot C)<x\cdot H,\end{eqnarray}$$
since
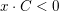 $x\cdot C<0$
by assumption and
$x\cdot C<0$
by assumption and
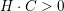 $H\cdot C>0$
by ampleness of
$H\cdot C>0$
by ampleness of
![]() $H$
. Therefore, if
$H$
. Therefore, if
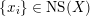 $\{x_{i}\}\in \operatorname{NS}(X)$
is as in assertion (ii), then
$\{x_{i}\}\in \operatorname{NS}(X)$
is as in assertion (ii), then
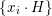 $\{x_{i}\cdot H\}$
is a strictly decreasing sequence of positive integers. In particular, it must be of finite length, and its last class must be nef.◻
$\{x_{i}\cdot H\}$
is a strictly decreasing sequence of positive integers. In particular, it must be of finite length, and its last class must be nef.◻
After these preparations, we obtain the following.
Proposition 4.5 (Termination of flops).
Let
![]() $(X,{\mathcal{L}})$
and
$(X,{\mathcal{L}})$
and
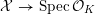 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
be as in Proposition 4.2. Then every sequence of flops as in Proposition 4.2 is finite. In particular, after a finite sequence
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
be as in Proposition 4.2. Then every sequence of flops as in Proposition 4.2 is finite. In particular, after a finite sequence
 $$\begin{eqnarray}({\mathcal{X}},{\mathcal{L}}){\dashrightarrow}({\mathcal{X}}^{+},{\mathcal{L}}^{+}){\dashrightarrow}({\mathcal{X}}^{+2},{\mathcal{L}}^{+2}){\dashrightarrow}\cdots {\dashrightarrow}({\mathcal{X}}^{+N},{\mathcal{L}}^{+N})\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{X}},{\mathcal{L}}){\dashrightarrow}({\mathcal{X}}^{+},{\mathcal{L}}^{+}){\dashrightarrow}({\mathcal{X}}^{+2},{\mathcal{L}}^{+2}){\dashrightarrow}\cdots {\dashrightarrow}({\mathcal{X}}^{+N},{\mathcal{L}}^{+N})\end{eqnarray}$$
of flops we arrive at a smooth model
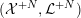 $({\mathcal{X}}^{+N},{\mathcal{L}}^{+N})$
of
$({\mathcal{X}}^{+N},{\mathcal{L}}^{+N})$
of
![]() $X$
over
$X$
over
![]() ${\mathcal{O}}_{K}$
such that the specialization
${\mathcal{O}}_{K}$
such that the specialization
![]() ${\mathcal{L}}_{0}^{+N}$
is big and nef.
${\mathcal{L}}_{0}^{+N}$
is big and nef.
Proof. Let
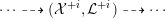 $\cdots {\dashrightarrow}({\mathcal{X}}^{+i},{\mathcal{L}}^{+i}){\dashrightarrow}\cdots \,$
be a sequence of flops in generalized
$\cdots {\dashrightarrow}({\mathcal{X}}^{+i},{\mathcal{L}}^{+i}){\dashrightarrow}\cdots \,$
be a sequence of flops in generalized
![]() $(-2)$
-curves
$(-2)$
-curves
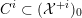 $C^{i}\subset ({\mathcal{X}}^{+i})_{0}$
as asserted by Proposition 4.2 and Lemma 4.3. Moreover, we have
$C^{i}\subset ({\mathcal{X}}^{+i})_{0}$
as asserted by Proposition 4.2 and Lemma 4.3. Moreover, we have
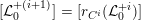 $[{\mathcal{L}}_{0}^{+(i+1)}]=[r_{C^{i}}({\mathcal{L}}_{0}^{+i})]$
by Lemma 4.3. By Lemma 4.4, this sequence is finite and
$[{\mathcal{L}}_{0}^{+(i+1)}]=[r_{C^{i}}({\mathcal{L}}_{0}^{+i})]$
by Lemma 4.3. By Lemma 4.4, this sequence is finite and
![]() ${\mathcal{L}}_{0}^{+N}$
is nef.◻
${\mathcal{L}}_{0}^{+N}$
is nef.◻
4.3 Morphism to a projective scheme
In the situation of Proposition 4.5, we obtain a birational morphism to a projective scheme as follows.
Proposition 4.6. Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
that admits a smooth model
$\unicode[STIX]{x1D714}_{X/K}$
that admits a smooth model
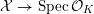 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Let
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
. Let
![]() ${\mathcal{L}}$
be an ample invertible sheaf on
${\mathcal{L}}$
be an ample invertible sheaf on
![]() $X$
and assume that
$X$
and assume that
![]() ${\mathcal{L}}_{0}$
is big and nef. Then the natural and a priori rational map
${\mathcal{L}}_{0}$
is big and nef. Then the natural and a priori rational map
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})\end{eqnarray}$$
is a morphism over
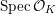 $\operatorname{Spec}{\mathcal{O}}_{K}$
to a projective scheme. More precisely:
$\operatorname{Spec}{\mathcal{O}}_{K}$
to a projective scheme. More precisely:
-
(i)
 $\unicode[STIX]{x1D70B}$
is a flopping contraction and induces an isomorphism of generic fibers;
$\unicode[STIX]{x1D70B}$
is a flopping contraction and induces an isomorphism of generic fibers; -
(ii) the induced morphism on special fibers
 $\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
is birational and contracts precisely those curves that have zero-intersection with
$\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
is birational and contracts precisely those curves that have zero-intersection with
 ${\mathcal{L}}_{0}$
. In particular,
${\mathcal{L}}_{0}$
. In particular,
 $({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
is a proper surface with at worst RDP singularities and
$({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
is a proper surface with at worst RDP singularities and
 $\unicode[STIX]{x1D70B}_{0}$
is the minimal resolution of singularities.
$\unicode[STIX]{x1D70B}_{0}$
is the minimal resolution of singularities.
Proof. Note that also
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial. Since
$\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial. Since
![]() ${\mathcal{L}}_{0}$
is big and nef, we obtain a proper and birational morphism
${\mathcal{L}}_{0}$
is big and nef, we obtain a proper and birational morphism
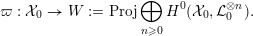 $$\begin{eqnarray}\unicode[STIX]{x1D71B}:{\mathcal{X}}_{0}\rightarrow W:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D71B}:{\mathcal{X}}_{0}\rightarrow W:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n}).\end{eqnarray}$$
Base-changing to
![]() $({\mathcal{X}}_{0})_{\overline{k}}$
, the induced morphism
$({\mathcal{X}}_{0})_{\overline{k}}$
, the induced morphism
![]() $\unicode[STIX]{x1D71B}_{\overline{k}}$
contracts an integral curve
$\unicode[STIX]{x1D71B}_{\overline{k}}$
contracts an integral curve
![]() $C$
if and only if it has zero-intersection with
$C$
if and only if it has zero-intersection with
![]() ${\mathcal{L}}_{0}$
. Since the intersection matrix formed by contracted curves is negative definite, and since an integral curve with negative self-intersection on a surface with numerically trivial canonical sheaf over an algebraically closed field is a
${\mathcal{L}}_{0}$
. Since the intersection matrix formed by contracted curves is negative definite, and since an integral curve with negative self-intersection on a surface with numerically trivial canonical sheaf over an algebraically closed field is a
![]() $(-2)$
-curve, it follows from the classification of Cartan matrices, that
$(-2)$
-curve, it follows from the classification of Cartan matrices, that
![]() $W_{\overline{k}}$
has at worst RDP singularities.
$W_{\overline{k}}$
has at worst RDP singularities.
Now,
![]() ${\mathcal{L}}_{0}^{\otimes n}$
is of degree
${\mathcal{L}}_{0}^{\otimes n}$
is of degree
![]() $0$
on contracted curves for all
$0$
on contracted curves for all
![]() $n$
, and over
$n$
, and over
![]() $\overline{k}$
, these curves are ADE curves. Thus we find
$\overline{k}$
, these curves are ADE curves. Thus we find
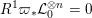 $R^{1}\unicode[STIX]{x1D71B}_{\ast }{\mathcal{L}}_{0}^{\otimes n}=0$
for all
$R^{1}\unicode[STIX]{x1D71B}_{\ast }{\mathcal{L}}_{0}^{\otimes n}=0$
for all
![]() $n\geqslant 0$
, which implies
$n\geqslant 0$
, which implies
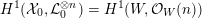 $H^{1}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n})=H^{1}(W,{\mathcal{O}}_{W}(n))$
for all
$H^{1}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n})=H^{1}(W,{\mathcal{O}}_{W}(n))$
for all
![]() $n\geqslant 0$
, and note that the latter term is zero for
$n\geqslant 0$
, and note that the latter term is zero for
![]() $n\gg 0$
by Serre vanishing. Replacing
$n\gg 0$
by Serre vanishing. Replacing
![]() ${\mathcal{L}}$
by some sufficiently high tensor power will not change
${\mathcal{L}}$
by some sufficiently high tensor power will not change
![]() $\unicode[STIX]{x1D71B}$
, and then we may assume that
$\unicode[STIX]{x1D71B}$
, and then we may assume that
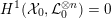 $H^{1}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n})=0$
for all
$H^{1}({\mathcal{X}}_{0},{\mathcal{L}}_{0}^{\otimes n})=0$
for all
![]() $n\geqslant 1$
. If
$n\geqslant 1$
. If
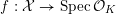 $f:{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
denotes the structure morphism, then semi-continuity and the previous vanishing result imply
$f:{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
denotes the structure morphism, then semi-continuity and the previous vanishing result imply
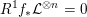 $R^{1}f_{\ast }{\mathcal{L}}^{\otimes n}=0$
for all
$R^{1}f_{\ast }{\mathcal{L}}^{\otimes n}=0$
for all
![]() $n\geqslant 1$
. Thus global sections of
$n\geqslant 1$
. Thus global sections of
![]() ${\mathcal{L}}_{0}^{\otimes n}$
extend to
${\mathcal{L}}_{0}^{\otimes n}$
extend to
![]() ${\mathcal{L}}^{\otimes n}$
, and since the former is globally generated for
${\mathcal{L}}^{\otimes n}$
, and since the former is globally generated for
![]() $n\gg 0$
so is the latter. Thus we obtain a morphism of algebraic spaces over
$n\gg 0$
so is the latter. Thus we obtain a morphism of algebraic spaces over
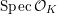 $\operatorname{Spec}{\mathcal{O}}_{K}$
$\operatorname{Spec}{\mathcal{O}}_{K}$
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n}).\end{eqnarray}$$
Since
![]() ${\mathcal{L}}$
is ample on
${\mathcal{L}}$
is ample on
![]() $X$
,
$X$
,
![]() $\unicode[STIX]{x1D70B}$
induces an isomorphism of generic fibers. Moreover, we can identify the induced map
$\unicode[STIX]{x1D70B}$
induces an isomorphism of generic fibers. Moreover, we can identify the induced map
![]() $\unicode[STIX]{x1D70B}_{0}$
on special fibers with
$\unicode[STIX]{x1D70B}_{0}$
on special fibers with
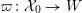 $\unicode[STIX]{x1D71B}:{\mathcal{X}}_{0}\rightarrow W$
from above.◻
$\unicode[STIX]{x1D71B}:{\mathcal{X}}_{0}\rightarrow W$
from above.◻
4.4 Birational relations among smooth models
As an application of existence and termination of flops, Kollár [Reference KollárKol89, Theorem 4.9] showed that any two birational complex threefolds with
![]() $\mathbb{Q}$
-factorial terminal singularities and nef canonical classes are connected by a finite sequence of flops.
$\mathbb{Q}$
-factorial terminal singularities and nef canonical classes are connected by a finite sequence of flops.
We have the following analog in our situation, but since we are dealing with algebraic spaces rather than projective schemes (which is analogous to the case of analytic threefolds in [Reference KollárKol89]), the flops as defined above do not suffice. We only show that two smooth models are connected by flopping contractions and their inverses.
Proposition 4.7. Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
that has good reduction. If
$\unicode[STIX]{x1D714}_{X/K}$
that has good reduction. If
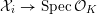 ${\mathcal{X}}_{i}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
are two smooth models of
${\mathcal{X}}_{i}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
are two smooth models of
![]() $X$
, then:
$X$
, then:
-
(i) the special fibers of
 ${\mathcal{X}}_{1}$
and
${\mathcal{X}}_{1}$
and
 ${\mathcal{X}}_{2}$
are isomorphic; and
${\mathcal{X}}_{2}$
are isomorphic; and -
(ii)
 ${\mathcal{X}}_{1}$
and
${\mathcal{X}}_{1}$
and
 ${\mathcal{X}}_{2}$
are connected by a sequence of birational rational maps that are compositions of flopping contractions and their inverses.
${\mathcal{X}}_{2}$
are connected by a sequence of birational rational maps that are compositions of flopping contractions and their inverses.
Proof. The special fibers of
![]() ${\mathcal{X}}_{1}$
and
${\mathcal{X}}_{1}$
and
![]() ${\mathcal{X}}_{2}$
are birational by the Matsusaka–Mumford theorem [Reference Matsusaka and MumfordMM64, Theorem 2], and since they are minimal surfaces of Kodaira dimension at least
${\mathcal{X}}_{2}$
are birational by the Matsusaka–Mumford theorem [Reference Matsusaka and MumfordMM64, Theorem 2], and since they are minimal surfaces of Kodaira dimension at least
![]() $0$
, they are isomorphic. (Note that this statement also follows from the much more detailed analysis below.)
$0$
, they are isomorphic. (Note that this statement also follows from the much more detailed analysis below.)
Now, choose an ample invertible sheaf
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $X$
. By Proposition 4.5, there exist finite sequences of flops
$X$
. By Proposition 4.5, there exist finite sequences of flops
 ${\mathcal{X}}_{i}{\dashrightarrow}\cdots {\dashrightarrow}{\mathcal{Y}}_{i}$
,
${\mathcal{X}}_{i}{\dashrightarrow}\cdots {\dashrightarrow}{\mathcal{Y}}_{i}$
,
![]() $i=1,2$
, such that
$i=1,2$
, such that
![]() ${\mathcal{L}}$
restricts to big and nef invertible sheaves on the special fibers of
${\mathcal{L}}$
restricts to big and nef invertible sheaves on the special fibers of
![]() ${\mathcal{Y}}_{i}$
.
${\mathcal{Y}}_{i}$
.
Applying Proposition 4.6 to our models
![]() ${\mathcal{Y}}_{i}$
, we obtain flopping contractions
${\mathcal{Y}}_{i}$
, we obtain flopping contractions
 $$\begin{eqnarray}{\mathcal{Y}}_{i}\rightarrow {\mathcal{Y}}_{i}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{Y}}_{i},{\mathcal{L}}^{\otimes n}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Y}}_{i}\rightarrow {\mathcal{Y}}_{i}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{Y}}_{i},{\mathcal{L}}^{\otimes n}).\end{eqnarray}$$
Now,
![]() ${\mathcal{L}}$
is ample on
${\mathcal{L}}$
is ample on
![]() ${\mathcal{Y}}_{i}^{\prime }$
. Moreover, the
${\mathcal{Y}}_{i}^{\prime }$
. Moreover, the
![]() ${\mathcal{Y}}_{i}^{\prime }$
are normal projective schemes and birational outside a finite number of curves in their special fibers. In fact, there exists a birational and rational map between them that is compatible with
${\mathcal{Y}}_{i}^{\prime }$
are normal projective schemes and birational outside a finite number of curves in their special fibers. In fact, there exists a birational and rational map between them that is compatible with
![]() ${\mathcal{L}}$
. Thus, by [Reference KovacsKov09, Theorem 5.14], this birational map extends to an isomorphism, and then we obtain a birational map
${\mathcal{L}}$
. Thus, by [Reference KovacsKov09, Theorem 5.14], this birational map extends to an isomorphism, and then we obtain a birational map
 ${\mathcal{Y}}_{1}{\dashrightarrow}{\mathcal{Y}}_{2}$
with decomposition
${\mathcal{Y}}_{1}{\dashrightarrow}{\mathcal{Y}}_{2}$
with decomposition
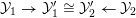 ${\mathcal{Y}}_{1}\rightarrow {\mathcal{Y}}_{1}^{\prime }\cong {\mathcal{Y}}_{2}^{\prime }\leftarrow {\mathcal{Y}}_{2}$
of the required form.
${\mathcal{Y}}_{1}\rightarrow {\mathcal{Y}}_{1}^{\prime }\cong {\mathcal{Y}}_{2}^{\prime }\leftarrow {\mathcal{Y}}_{2}$
of the required form.
Putting all these birational modifications together, we have connected
![]() ${\mathcal{X}}_{1}$
and
${\mathcal{X}}_{1}$
and
![]() ${\mathcal{X}}_{2}$
by a sequence of birational maps of the required form.◻
${\mathcal{X}}_{2}$
by a sequence of birational maps of the required form.◻
5 Group actions on models
In this section, we study group actions on models. More precisely, we are given a smooth and proper surface
![]() $X$
over
$X$
over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
, a finite field extension
$\unicode[STIX]{x1D714}_{X/K}$
, a finite field extension
![]() $L/K$
, which is Galois with group
$L/K$
, which is Galois with group
![]() $G$
, and a smooth proper model
$G$
, and a smooth proper model
 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
![]() $X_{L}$
. Then we study the following questions.
$X_{L}$
. Then we study the following questions.
-
(i) Does the
 $G$
-action on
$G$
-action on
 $X_{L}$
extend to
$X_{L}$
extend to
 ${\mathcal{X}}$
?
${\mathcal{X}}$
? -
(ii) If so, is the special fiber
 $({\mathcal{X}}/G)_{0}$
of the quotient equal to the quotient
$({\mathcal{X}}/G)_{0}$
of the quotient equal to the quotient
 ${\mathcal{X}}_{0}/G$
of the special fiber?
${\mathcal{X}}_{0}/G$
of the special fiber?
It turns out, that the answer to question (i) is ‘yes’, when allowing certain birational modifications of the model, and in question (ii), it turns out that the case where
![]() $p\neq 0$
and
$p\neq 0$
and
![]() $p$
divides the order of
$p$
divides the order of
![]() $G$
(wild group actions) is subtle.
$G$
(wild group actions) is subtle.
5.1 Extending group actions to a possibly singular model
Given a smooth and proper surface
![]() $X$
over
$X$
over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
that admits a model
$\unicode[STIX]{x1D714}_{X/K}$
that admits a model
![]() ${\mathcal{X}}$
with good reduction after a finite Galois extension
${\mathcal{X}}$
with good reduction after a finite Galois extension
![]() $L/K$
with group
$L/K$
with group
![]() $G$
, we first show that the
$G$
, we first show that the
![]() $G$
-action extends to a (mild) birational modification of
$G$
-action extends to a (mild) birational modification of
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
Proposition 5.1. Let
![]() $X$
be a smooth and proper surface over
$X$
be a smooth and proper surface over
![]() $K$
with numerically trivial
$K$
with numerically trivial
![]() $\unicode[STIX]{x1D714}_{X/K}$
. Assume that there exist:
$\unicode[STIX]{x1D714}_{X/K}$
. Assume that there exist:
-
(i) a finite Galois extension
 $L/K$
with Galois group
$L/K$
with Galois group
 $G$
; as well as
$G$
; as well as -
(ii) a smooth model
 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
of
 $X_{L}$
; and
$X_{L}$
; and -
(iii) an ample invertible sheaf
 ${\mathcal{L}}$
on
${\mathcal{L}}$
on
 $X$
, whose pull-back to
$X$
, whose pull-back to
 $X_{L}$
restricts to an invertible sheaf on the special fiber
$X_{L}$
restricts to an invertible sheaf on the special fiber
 ${\mathcal{X}}_{0}$
that is big and nef.
${\mathcal{X}}_{0}$
that is big and nef.
Then there exists a proper birational morphism
![]() $\unicode[STIX]{x1D70B}$
$\unicode[STIX]{x1D70B}$
of algebraic spaces over
![]() ${\mathcal{O}}_{L}$
, such that the following hold.
${\mathcal{O}}_{L}$
, such that the following hold.
-
(i) The natural
 $G$
-action on
$G$
-action on
 $X_{L}$
extends to
$X_{L}$
extends to
 ${\mathcal{X}}^{\prime }$
and is compatible with the
${\mathcal{X}}^{\prime }$
and is compatible with the
 $G$
-action on
$G$
-action on
 ${\mathcal{O}}_{L}$
.
${\mathcal{O}}_{L}$
. -
(ii) The algebraic space
 ${\mathcal{X}}^{\prime }$
is a projective scheme over
${\mathcal{X}}^{\prime }$
is a projective scheme over
 $\operatorname{Spec}{\mathcal{O}}_{L}$
.
$\operatorname{Spec}{\mathcal{O}}_{L}$
. -
(iii) The generic fibers of
 ${\mathcal{X}}$
and
${\mathcal{X}}$
and
 ${\mathcal{X}}^{\prime }$
are isomorphic via
${\mathcal{X}}^{\prime }$
are isomorphic via
 $\unicode[STIX]{x1D70B}$
, whereas the induced morphism on special fibers
$\unicode[STIX]{x1D70B}$
, whereas the induced morphism on special fibers
 $\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
is birational and projective, such that the geometric special fiber
$\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
is birational and projective, such that the geometric special fiber
 $({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has at worst RDP singularities.
$({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has at worst RDP singularities.
Moreover, if
![]() $\unicode[STIX]{x1D70B}$
is not an isomorphism, then
$\unicode[STIX]{x1D70B}$
is not an isomorphism, then
![]() ${\mathcal{X}}^{\prime }$
is not regular.
${\mathcal{X}}^{\prime }$
is not regular.
Proof. Since
![]() ${\mathcal{X}}$
is regular, the pull-back of
${\mathcal{X}}$
is regular, the pull-back of
![]() ${\mathcal{L}}$
to
${\mathcal{L}}$
to
![]() $X_{L}$
extends to an invertible sheaf on
$X_{L}$
extends to an invertible sheaf on
![]() ${\mathcal{X}}$
. By abuse of notation, we shall denote the pull-back to
${\mathcal{X}}$
. By abuse of notation, we shall denote the pull-back to
![]() $X_{L}$
and its extension to
$X_{L}$
and its extension to
![]() ${\mathcal{X}}$
again by
${\mathcal{X}}$
again by
![]() ${\mathcal{L}}$
. By assumption, the restriction
${\mathcal{L}}$
. By assumption, the restriction
![]() ${\mathcal{L}}_{0}$
of
${\mathcal{L}}_{0}$
of
![]() ${\mathcal{L}}$
to the special fiber
${\mathcal{L}}$
to the special fiber
![]() ${\mathcal{X}}_{0}$
is big and nef. Note that
${\mathcal{X}}_{0}$
is big and nef. Note that
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial. Let
$\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
is numerically trivial. Let
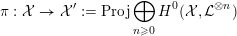 $$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})\end{eqnarray}$$
be the morphism of algebraic spaces over
![]() ${\mathcal{O}}_{L}$
given by Proposition 4.6. Then
${\mathcal{O}}_{L}$
given by Proposition 4.6. Then
![]() $\unicode[STIX]{x1D70B}$
has all the properties asserted in claim (iii) of the proposition. Clearly,
$\unicode[STIX]{x1D70B}$
has all the properties asserted in claim (iii) of the proposition. Clearly,
![]() ${\mathcal{X}}^{\prime }$
is a projective scheme over
${\mathcal{X}}^{\prime }$
is a projective scheme over
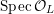 $\operatorname{Spec}{\mathcal{O}}_{L}$
, and if
$\operatorname{Spec}{\mathcal{O}}_{L}$
, and if
![]() $\unicode[STIX]{x1D70B}$
is not an isomorphism, then the exceptional locus is non-empty and of codimension
$\unicode[STIX]{x1D70B}$
is not an isomorphism, then the exceptional locus is non-empty and of codimension
![]() $2$
, which implies that
$2$
, which implies that
![]() ${\mathcal{X}}^{\prime }$
cannot be regular by van der Waerden purity; see, for example, [Reference LiuLiu02, Theorem 7.2.22].
${\mathcal{X}}^{\prime }$
cannot be regular by van der Waerden purity; see, for example, [Reference LiuLiu02, Theorem 7.2.22].
It remains to establish the
![]() $G$
-action on
$G$
-action on
![]() ${\mathcal{X}}^{\prime }$
. Since
${\mathcal{X}}^{\prime }$
. Since
![]() ${\mathcal{L}}$
is a
${\mathcal{L}}$
is a
![]() $G$
-invariant invertible sheaf on
$G$
-invariant invertible sheaf on
![]() $X_{L}$
, we have an induced
$X_{L}$
, we have an induced
![]() $G$
-action on
$G$
-action on
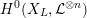 $H^{0}(X_{L},{\mathcal{L}}^{\otimes n})$
for all
$H^{0}(X_{L},{\mathcal{L}}^{\otimes n})$
for all
![]() $n\geqslant 0$
. We will show that this extends to an action on
$n\geqslant 0$
. We will show that this extends to an action on
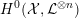 $H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})$
. First, we show that there exists a closed subspace
$H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})$
. First, we show that there exists a closed subspace
![]() ${\mathcal{Z}}\subset {\mathcal{X}}$
of codimension at least
${\mathcal{Z}}\subset {\mathcal{X}}$
of codimension at least
![]() $2$
that is contained in
$2$
that is contained in
![]() ${\mathcal{X}}_{0}$
, such that the
${\mathcal{X}}_{0}$
, such that the
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
extends to an action on
$X_{L}$
extends to an action on
 ${\mathcal{U}}:={\mathcal{X}}\setminus {\mathcal{Z}}$
. Since every birational rational map between two normal algebraic spaces is an isomorphism outside a closed subspace of codimension at least
${\mathcal{U}}:={\mathcal{X}}\setminus {\mathcal{Z}}$
. Since every birational rational map between two normal algebraic spaces is an isomorphism outside a closed subspace of codimension at least
![]() $2$
, there exists for every
$2$
, there exists for every
![]() $g\in G$
a closed subspace
$g\in G$
a closed subspace
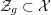 ${\mathcal{Z}}_{g}\subset {\mathcal{X}}$
of codimension at least
${\mathcal{Z}}_{g}\subset {\mathcal{X}}$
of codimension at least
![]() $2$
that is contained in
$2$
that is contained in
![]() ${\mathcal{X}}_{0}$
and such that
${\mathcal{X}}_{0}$
and such that
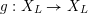 $g:X_{L}\rightarrow X_{L}$
extends to
$g:X_{L}\rightarrow X_{L}$
extends to
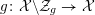 $g:{\mathcal{X}}\setminus {\mathcal{Z}}_{g}\rightarrow {\mathcal{X}}$
. Since
$g:{\mathcal{X}}\setminus {\mathcal{Z}}_{g}\rightarrow {\mathcal{X}}$
. Since
![]() ${\mathcal{X}}_{0}$
is a minimal surface, the restriction
${\mathcal{X}}_{0}$
is a minimal surface, the restriction
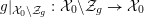 $g|_{{\mathcal{X}}_{0}\setminus {\mathcal{Z}}_{g}}:{\mathcal{X}}_{0}\setminus {\mathcal{Z}}_{g}\rightarrow {\mathcal{X}}_{0}$
to the special fiber extends to an automorphism
$g|_{{\mathcal{X}}_{0}\setminus {\mathcal{Z}}_{g}}:{\mathcal{X}}_{0}\setminus {\mathcal{Z}}_{g}\rightarrow {\mathcal{X}}_{0}$
to the special fiber extends to an automorphism
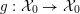 $g:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}$
. This defines a
$g:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}$
. This defines a
![]() $G$
-action on
$G$
-action on
![]() ${\mathcal{X}}_{0}$
. Let
${\mathcal{X}}_{0}$
. Let
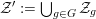 ${\mathcal{Z}}^{\prime }:=\bigcup _{g\in G}{\mathcal{Z}}_{g}$
and
${\mathcal{Z}}^{\prime }:=\bigcup _{g\in G}{\mathcal{Z}}_{g}$
and
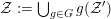 ${\mathcal{Z}}:=\bigcup _{g\in G}g({\mathcal{Z}}^{\prime })$
, where
${\mathcal{Z}}:=\bigcup _{g\in G}g({\mathcal{Z}}^{\prime })$
, where
![]() $g({\mathcal{Z}}^{\prime })$
is the image by the action just defined. Since
$g({\mathcal{Z}}^{\prime })$
is the image by the action just defined. Since
![]() $G$
is a finite group,
$G$
is a finite group,
![]() ${\mathcal{Z}}$
is closed. This
${\mathcal{Z}}$
is closed. This
![]() ${\mathcal{Z}}$
satisfies the above condition, for otherwise there exists a
${\mathcal{Z}}$
satisfies the above condition, for otherwise there exists a
![]() $g\in G$
, such that the image of
$g\in G$
, such that the image of
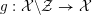 $g:{\mathcal{X}}\setminus {\mathcal{Z}}\rightarrow {\mathcal{X}}$
is not contained in
$g:{\mathcal{X}}\setminus {\mathcal{Z}}\rightarrow {\mathcal{X}}$
is not contained in
![]() ${\mathcal{X}}\setminus {\mathcal{Z}}$
, or, equivalently
${\mathcal{X}}\setminus {\mathcal{Z}}$
, or, equivalently
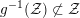 $g^{-1}({\mathcal{Z}})\not \subset {\mathcal{Z}}$
. However, since
$g^{-1}({\mathcal{Z}})\not \subset {\mathcal{Z}}$
. However, since
![]() ${\mathcal{Z}}$
is
${\mathcal{Z}}$
is
![]() $G$
-stable, this cannot happen. Thus we obtain a
$G$
-stable, this cannot happen. Thus we obtain a
![]() $G$
-action on
$G$
-action on
 ${\mathcal{U}}={\mathcal{X}}\setminus {\mathcal{Z}}$
.
${\mathcal{U}}={\mathcal{X}}\setminus {\mathcal{Z}}$
.
If
![]() $s$
is a global section of
$s$
is a global section of
![]() ${\mathcal{L}}^{\otimes n}$
over
${\mathcal{L}}^{\otimes n}$
over
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() $\unicode[STIX]{x1D70E}\in G$
, then
$\unicode[STIX]{x1D70E}\in G$
, then
![]() $\unicode[STIX]{x1D70E}(s|_{{\mathcal{U}}})$
is a well-defined global section of
$\unicode[STIX]{x1D70E}(s|_{{\mathcal{U}}})$
is a well-defined global section of
![]() ${\mathcal{L}}^{\otimes n}$
over
${\mathcal{L}}^{\otimes n}$
over
 ${\mathcal{U}}={\mathcal{X}}\setminus {\mathcal{Z}}$
. Since
${\mathcal{U}}={\mathcal{X}}\setminus {\mathcal{Z}}$
. Since
![]() ${\mathcal{L}}^{\otimes n}$
is a reflexive sheaf on a regular algebraic space,
${\mathcal{L}}^{\otimes n}$
is a reflexive sheaf on a regular algebraic space,
![]() $\unicode[STIX]{x1D70E}(s|_{{\mathcal{U}}})$
extends uniquely to a global section of
$\unicode[STIX]{x1D70E}(s|_{{\mathcal{U}}})$
extends uniquely to a global section of
![]() ${\mathcal{L}}^{\otimes n}$
over
${\mathcal{L}}^{\otimes n}$
over
![]() ${\mathcal{X}}$
. Thus we obtain a
${\mathcal{X}}$
. Thus we obtain a
![]() $G$
-action on
$G$
-action on
 $H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})$
, which gives rise to a
$H^{0}({\mathcal{X}},{\mathcal{L}}^{\otimes n})$
, which gives rise to a
![]() $G$
-action on
$G$
-action on
![]() ${\mathcal{X}}^{\prime }$
that is compatible with the
${\mathcal{X}}^{\prime }$
that is compatible with the
![]() $G$
-action on
$G$
-action on
![]() ${\mathcal{O}}_{L}$
, as well as with the natural
${\mathcal{O}}_{L}$
, as well as with the natural
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
.◻
$X_{L}$
.◻
Remark 5.2. If all assumptions of Proposition 5.1 except assumption (iii) are satisfied, then Proposition 4.5 shows that there exists another smooth model of
![]() $X$
over
$X$
over
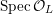 $\operatorname{Spec}{\mathcal{O}}_{L}$
for which all assumptions including assumption (iii) hold, and to which we can apply Proposition 5.1.
$\operatorname{Spec}{\mathcal{O}}_{L}$
for which all assumptions including assumption (iii) hold, and to which we can apply Proposition 5.1.
5.2 Examples where the action does not extend
In general, it is too much to ask for an extension of the
![]() $G$
-action from
$G$
-action from
![]() $X_{L}$
to
$X_{L}$
to
![]() ${\mathcal{X}}$
(notation as in Proposition 5.1). The following example is typical.
${\mathcal{X}}$
(notation as in Proposition 5.1). The following example is typical.
Example 5.3 (Arithmetic
 $3$
-fold flop).
$3$
-fold flop).
Consider
![]() $\mathbb{Q}_{p}$
with
$\mathbb{Q}_{p}$
with
![]() $p\neq 2$
and set
$p\neq 2$
and set
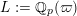 $L:=\mathbb{Q}_{p}(\unicode[STIX]{x1D71B})$
, where
$L:=\mathbb{Q}_{p}(\unicode[STIX]{x1D71B})$
, where
![]() $\unicode[STIX]{x1D71B}^{2}=p$
. Then
$\unicode[STIX]{x1D71B}^{2}=p$
. Then
![]() $L/\mathbb{Q}_{p}$
is Galois with group
$L/\mathbb{Q}_{p}$
is Galois with group
 $G=\mathbb{Z}/2\mathbb{Z}$
and the non-trivial element of
$G=\mathbb{Z}/2\mathbb{Z}$
and the non-trivial element of
![]() $G$
acts as
$G$
acts as
 $\unicode[STIX]{x1D71B}\mapsto -\unicode[STIX]{x1D71B}$
. We equip
$\unicode[STIX]{x1D71B}\mapsto -\unicode[STIX]{x1D71B}$
. We equip
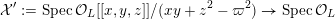 $$\begin{eqnarray}{\mathcal{X}}^{\prime }:=\operatorname{Spec}{\mathcal{O}}_{L}[[x,y,z]]/(xy+z^{2}-\unicode[STIX]{x1D71B}^{2})\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}^{\prime }:=\operatorname{Spec}{\mathcal{O}}_{L}[[x,y,z]]/(xy+z^{2}-\unicode[STIX]{x1D71B}^{2})\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}\end{eqnarray}$$
with the
![]() $G$
-action that is the Galois action on
$G$
-action that is the Galois action on
![]() ${\mathcal{O}}_{L}$
, and that is trivial on
${\mathcal{O}}_{L}$
, and that is trivial on
![]() $x,y,z$
. It is easy to see that the induced
$x,y,z$
. It is easy to see that the induced
![]() $G$
-action on the special fiber
$G$
-action on the special fiber
![]() ${\mathcal{X}}_{0}^{\prime }$
is trivial. Next, we consider the two ideal sheaves
${\mathcal{X}}_{0}^{\prime }$
is trivial. Next, we consider the two ideal sheaves
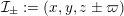 ${\mathcal{I}}_{\pm }:=(x,y,z\pm \unicode[STIX]{x1D71B})$
of
${\mathcal{I}}_{\pm }:=(x,y,z\pm \unicode[STIX]{x1D71B})$
of
![]() ${\mathcal{O}}_{{\mathcal{X}}^{\prime }}$
and their blow-ups
${\mathcal{O}}_{{\mathcal{X}}^{\prime }}$
and their blow-ups
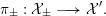 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\pm }:{\mathcal{X}}_{\pm }\longrightarrow {\mathcal{X}}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\pm }:{\mathcal{X}}_{\pm }\longrightarrow {\mathcal{X}}^{\prime }.\end{eqnarray}$$
Then
![]() ${\mathcal{X}}_{\pm }$
are regular schemes,
${\mathcal{X}}_{\pm }$
are regular schemes,
![]() ${\mathcal{X}}^{\prime }$
is singular at the closed point
${\mathcal{X}}^{\prime }$
is singular at the closed point
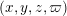 $(x,y,z,\unicode[STIX]{x1D71B})$
,
$(x,y,z,\unicode[STIX]{x1D71B})$
,
![]() $\unicode[STIX]{x1D70B}_{\pm }$
are both resolutions of singularities, and the exceptional locus is a
$\unicode[STIX]{x1D70B}_{\pm }$
are both resolutions of singularities, and the exceptional locus is a
![]() $\mathbb{P}^{1}$
in both cases. The ideals
$\mathbb{P}^{1}$
in both cases. The ideals
![]() ${\mathcal{I}}_{\pm }$
are not
${\mathcal{I}}_{\pm }$
are not
![]() $G$
-invariant and the
$G$
-invariant and the
![]() $G$
-action on
$G$
-action on
![]() ${\mathcal{X}}^{\prime }$
does not extend to that on
${\mathcal{X}}^{\prime }$
does not extend to that on
![]() ${\mathcal{X}}_{+}$
nor on
${\mathcal{X}}_{+}$
nor on
![]() ${\mathcal{X}}_{-}$
. (Instead, the non-trivial element of
${\mathcal{X}}_{-}$
. (Instead, the non-trivial element of
![]() $G$
induces an isomorphism
$G$
induces an isomorphism
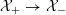 ${\mathcal{X}}_{+}\rightarrow {\mathcal{X}}_{-}$
.) In fact,
${\mathcal{X}}_{+}\rightarrow {\mathcal{X}}_{-}$
.) In fact,
![]() ${\mathcal{X}}^{\prime }$
is an arithmetic version of a
${\mathcal{X}}^{\prime }$
is an arithmetic version of a
![]() $3$
-fold ordinary double point, and the rational map
$3$
-fold ordinary double point, and the rational map
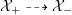 ${\mathcal{X}}_{+}{\dashrightarrow}{\mathcal{X}}_{-}$
is an arithmetic version of the classical Atiyah flop.
${\mathcal{X}}_{+}{\dashrightarrow}{\mathcal{X}}_{-}$
is an arithmetic version of the classical Atiyah flop.
Even worse, the following example (which is a modification of Example 7.1 below, and rests on examples from [Reference MatsumotoMat15, §5.3] and [Reference van LuijkvanL07, §3]) shows that if we have a
![]() $G$
-action on a singular model
$G$
-action on a singular model
![]() ${\mathcal{X}}^{\prime }$
as in Proposition 5.1, then there may exist resolutions of singularities to which the
${\mathcal{X}}^{\prime }$
as in Proposition 5.1, then there may exist resolutions of singularities to which the
![]() $G$
-action extends, as well as resolutions to which the
$G$
-action extends, as well as resolutions to which the
![]() $G$
-action does not extend. Moreover, our examples are models of K3 surfaces, that is, such phenomena are highly relevant for our discussion.
$G$
-action does not extend. Moreover, our examples are models of K3 surfaces, that is, such phenomena are highly relevant for our discussion.
Example 5.4. Before giving explicit examples, let us explain the strategy, again, for
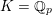 $K=\mathbb{Q}_{p}$
and
$K=\mathbb{Q}_{p}$
and
![]() $k=\mathbb{F}_{p}$
in this example.
$k=\mathbb{F}_{p}$
in this example.
Assume
![]() $p\neq 2$
, let
$p\neq 2$
, let
![]() $k^{\prime }/k$
be the unique extension of degree
$k^{\prime }/k$
be the unique extension of degree
![]() $2$
, let
$2$
, let
![]() $K^{\prime }/K$
be the corresponding unramified extension, and let
$K^{\prime }/K$
be the corresponding unramified extension, and let
 $G=\{1,\unicode[STIX]{x1D70E}\}$
be the Galois group of both extensions. Next, let
$G=\{1,\unicode[STIX]{x1D70E}\}$
be the Galois group of both extensions. Next, let
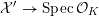 ${\mathcal{X}}^{\prime }\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
be a proper scheme such that the geometric special fiber
${\mathcal{X}}^{\prime }\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
be a proper scheme such that the geometric special fiber
![]() $({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has only RDP singularities and at least two of them. Set
$({\mathcal{X}}_{0}^{\prime })_{\overline{k}}$
has only RDP singularities and at least two of them. Set
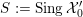 $S:=\operatorname{Sing}{\mathcal{X}}_{0}^{\prime }$
, and assume that all points of
$S:=\operatorname{Sing}{\mathcal{X}}_{0}^{\prime }$
, and assume that all points of
![]() $S$
are
$S$
are
![]() $k^{\prime }$
-rational but not all
$k^{\prime }$
-rational but not all
![]() $k$
-rational. Then
$k$
-rational. Then
![]() $G$
acts non-trivially on
$G$
acts non-trivially on
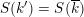 $S(k^{\prime })=S(\overline{k})$
. Let us finally assume that there exist two different resolutions of singularities
$S(k^{\prime })=S(\overline{k})$
. Let us finally assume that there exist two different resolutions of singularities
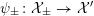 $\unicode[STIX]{x1D713}_{\pm }:{\mathcal{X}}_{\pm }\rightarrow {\mathcal{X}}^{\prime }$
, both of which are isomorphisms outside
$\unicode[STIX]{x1D713}_{\pm }:{\mathcal{X}}_{\pm }\rightarrow {\mathcal{X}}^{\prime }$
, both of which are isomorphisms outside
![]() $S$
, and both of which are obtained by blowing up ideal sheaves
$S$
, and both of which are obtained by blowing up ideal sheaves
![]() ${\mathcal{I}}_{\pm }$
defined over
${\mathcal{I}}_{\pm }$
defined over
![]() ${\mathcal{O}}_{K}$
. From this setup, we can produce the announced counterexamples.
${\mathcal{O}}_{K}$
. From this setup, we can produce the announced counterexamples.
-
(i) The Galois action on
 $({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
extends to
$({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
extends to
 $({\mathcal{X}}_{+})_{{\mathcal{O}}_{K^{\prime }}}$
, as well as to
$({\mathcal{X}}_{+})_{{\mathcal{O}}_{K^{\prime }}}$
, as well as to
 $({\mathcal{X}}_{-})_{{\mathcal{O}}_{K^{\prime }}}$
. Thus there do exist resolutions of singularities to which the
$({\mathcal{X}}_{-})_{{\mathcal{O}}_{K^{\prime }}}$
. Thus there do exist resolutions of singularities to which the
 $G$
-action extends.
$G$
-action extends. -
(ii) On the other hand, for each decomposition
 $S(k^{\prime })=S_{1}\sqcup S_{2}$
, we define
$S(k^{\prime })=S_{1}\sqcup S_{2}$
, we define
 $\unicode[STIX]{x1D713}_{S_{1},S_{2}}:{\mathcal{X}}_{S_{1},S_{2}}\rightarrow ({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
to be the morphism that is equal to
$\unicode[STIX]{x1D713}_{S_{1},S_{2}}:{\mathcal{X}}_{S_{1},S_{2}}\rightarrow ({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
to be the morphism that is equal to
 $\unicode[STIX]{x1D713}_{+}$
(respectively
$\unicode[STIX]{x1D713}_{+}$
(respectively
 $\unicode[STIX]{x1D713}_{-}$
) on
$\unicode[STIX]{x1D713}_{-}$
) on
 $({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}\setminus S_{2}$
(respectively on
$({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}\setminus S_{2}$
(respectively on
 $({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}\setminus S_{1}$
). We note that
$({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}\setminus S_{1}$
). We note that
 $\unicode[STIX]{x1D713}_{S_{1},S_{2}}$
is also a resolution of singularities. But now, if
$\unicode[STIX]{x1D713}_{S_{1},S_{2}}$
is also a resolution of singularities. But now, if
 $S_{1}$
and
$S_{1}$
and
 $S_{2}$
are not
$S_{2}$
are not
 $G$
-stable, then the
$G$
-stable, then the
 $G$
-action on
$G$
-action on
 $({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
does not extend to
$({\mathcal{X}}^{\prime })_{{\mathcal{O}}_{K^{\prime }}}$
does not extend to
 ${\mathcal{X}}_{S_{1},S_{2}}$
, but induces an isomorphism from
${\mathcal{X}}_{S_{1},S_{2}}$
, but induces an isomorphism from
 ${\mathcal{X}}_{S_{1},S_{2}}$
to
${\mathcal{X}}_{S_{1},S_{2}}$
to
 ${\mathcal{X}}_{\unicode[STIX]{x1D70E}(S_{1}),\unicode[STIX]{x1D70E}(S_{2})}$
, where
${\mathcal{X}}_{\unicode[STIX]{x1D70E}(S_{1}),\unicode[STIX]{x1D70E}(S_{2})}$
, where
 $\unicode[STIX]{x1D70E}\in G$
is the non-trivial element.
$\unicode[STIX]{x1D70E}\in G$
is the non-trivial element.
We now give explicit examples for
![]() $p\geqslant 5$
and
$p\geqslant 5$
and
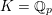 $K=\mathbb{Q}_{p}$
. Fix a prime
$K=\mathbb{Q}_{p}$
. Fix a prime
![]() $p\geqslant 5$
and choose an integer
$p\geqslant 5$
and choose an integer
![]() $d$
such that
$d$
such that
![]() $d$
is not a quadratic residue modulo
$d$
is not a quadratic residue modulo
![]() $p$
, and such that
$p$
, and such that
 $d^{6}\not \equiv -2^{-4}\cdot 3^{-3}~\text{mod}~p$
(one easily checks that such
$d^{6}\not \equiv -2^{-4}\cdot 3^{-3}~\text{mod}~p$
(one easily checks that such
![]() $d$
exists). We define the polynomial
$d$
exists). We define the polynomial
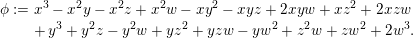 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719} & := & \displaystyle x^{3}-x^{2}y-x^{2}z+x^{2}w-xy^{2}-xyz+2xyw+xz^{2}+2xzw\nonumber\\ \displaystyle & & \displaystyle +\,y^{3}+y^{2}z-y^{2}w+yz^{2}+yzw-yw^{2}+z^{2}w+zw^{2}+2w^{3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719} & := & \displaystyle x^{3}-x^{2}y-x^{2}z+x^{2}w-xy^{2}-xyz+2xyw+xz^{2}+2xzw\nonumber\\ \displaystyle & & \displaystyle +\,y^{3}+y^{2}z-y^{2}w+yz^{2}+yzw-yw^{2}+z^{2}w+zw^{2}+2w^{3}.\nonumber\end{eqnarray}$$
Then we choose a homogeneous polynomial
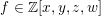 $f\in \mathbb{Z}[x,y,z,w]$
of degree
$f\in \mathbb{Z}[x,y,z,w]$
of degree
![]() $3$
, such that the following congruences hold:
$3$
, such that the following congruences hold:
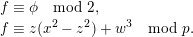 $$\begin{eqnarray}\displaystyle f & \equiv & \displaystyle \unicode[STIX]{x1D719}\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle f & \equiv & \displaystyle z(x^{2}-z^{2})+w^{3}\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f & \equiv & \displaystyle \unicode[STIX]{x1D719}\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle f & \equiv & \displaystyle z(x^{2}-z^{2})+w^{3}\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
Next, we choose homogeneous quadratic polynomials
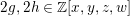 $2g,2h\in \mathbb{Z}[x,y,z,w]$
, such that the following congruences hold:
$2g,2h\in \mathbb{Z}[x,y,z,w]$
, such that the following congruences hold:
 $$\begin{eqnarray}\displaystyle g^{2}-p^{2}h^{2} & \equiv & \displaystyle (z^{2}+xy+yz)(z^{2}+xy)\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle g^{2}-p^{2}h^{2} & \equiv & \displaystyle (y^{2}-dx^{2})^{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g^{2}-p^{2}h^{2} & \equiv & \displaystyle (z^{2}+xy+yz)(z^{2}+xy)\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle g^{2}-p^{2}h^{2} & \equiv & \displaystyle (y^{2}-dx^{2})^{2}\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
Finally, we define the quartic hypersurface
 $$\begin{eqnarray}{\mathcal{X}}^{\prime }:={\mathcal{X}}^{\prime }(p):=\{wf+g^{2}-p^{2}h^{2}=0\}\subset \mathbb{P}_{\mathbb{ Z}_{p}}^{3},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}^{\prime }:={\mathcal{X}}^{\prime }(p):=\{wf+g^{2}-p^{2}h^{2}=0\}\subset \mathbb{P}_{\mathbb{ Z}_{p}}^{3},\end{eqnarray}$$
and denote by
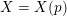 $X=X(p)$
its generic fiber. Then
$X=X(p)$
its generic fiber. Then
![]() $X$
is a smooth K3 surface over
$X$
is a smooth K3 surface over
![]() $\mathbb{Q}_{p}$
. The subscheme
$\mathbb{Q}_{p}$
. The subscheme
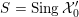 $S=\operatorname{Sing}{\mathcal{X}}_{0}^{\prime }$
is given by
$S=\operatorname{Sing}{\mathcal{X}}_{0}^{\prime }$
is given by
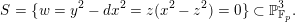 $$\begin{eqnarray}S=\{w=y^{2}-dx^{2}=z(x^{2}-z^{2})=0\}\subset \mathbb{P}_{\mathbb{ F}_{p}}^{3}.\end{eqnarray}$$
$$\begin{eqnarray}S=\{w=y^{2}-dx^{2}=z(x^{2}-z^{2})=0\}\subset \mathbb{P}_{\mathbb{ F}_{p}}^{3}.\end{eqnarray}$$
Thus we find six RDP singularities on
![]() $({\mathcal{X}}_{0}^{\prime })_{\overline{\mathbb{F}}_{p}}$
, all of which are defined over
$({\mathcal{X}}_{0}^{\prime })_{\overline{\mathbb{F}}_{p}}$
, all of which are defined over
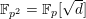 $\mathbb{F}_{p^{2}}=\mathbb{F}_{p}[\sqrt{d}]$
, and
$\mathbb{F}_{p^{2}}=\mathbb{F}_{p}[\sqrt{d}]$
, and
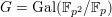 $G=\operatorname{Gal}(\mathbb{F}_{p^{2}}/\mathbb{F}_{p})$
acts non-trivially on
$G=\operatorname{Gal}(\mathbb{F}_{p^{2}}/\mathbb{F}_{p})$
acts non-trivially on
![]() $S(k^{\prime })$
, since
$S(k^{\prime })$
, since
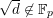 $\sqrt{d}\not \in \mathbb{F}_{p}$
. Finally, the blow-ups
$\sqrt{d}\not \in \mathbb{F}_{p}$
. Finally, the blow-ups
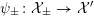 $\unicode[STIX]{x1D713}_{\pm }:{\mathcal{X}}_{\pm }\rightarrow {\mathcal{X}}^{\prime }$
of the ideals
$\unicode[STIX]{x1D713}_{\pm }:{\mathcal{X}}_{\pm }\rightarrow {\mathcal{X}}^{\prime }$
of the ideals
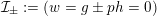 ${\mathcal{I}}_{\pm }:=(w=g\pm ph=0)$
are both resolutions of singularities. As explained in the strategy above, this setup yields the desired examples. (We refer to Remark 7.3 for the reason why we use this
${\mathcal{I}}_{\pm }:=(w=g\pm ph=0)$
are both resolutions of singularities. As explained in the strategy above, this setup yields the desired examples. (We refer to Remark 7.3 for the reason why we use this
![]() $\unicode[STIX]{x1D719}$
.)
$\unicode[STIX]{x1D719}$
.)
5.3 Extending the inertia action to the smooth model
Despite all these discouraging examples, there are situations, in which the
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
does extend to
$X_{L}$
does extend to
![]() ${\mathcal{X}}$
, and not merely to a singular model
${\mathcal{X}}$
, and not merely to a singular model
![]() ${\mathcal{X}}^{\prime }$
(notation as in Proposition 5.1). More precisely, we have the following result.
${\mathcal{X}}^{\prime }$
(notation as in Proposition 5.1). More precisely, we have the following result.
Proposition 5.5. We keep the notation and assumptions of Proposition 5.1.
-
(i) If
 $X$
is an Abelian surface or a hyperelliptic surface, then the
$X$
is an Abelian surface or a hyperelliptic surface, then the
 $G$
-action on
$G$
-action on
 $X_{L}$
extends to
$X_{L}$
extends to
 ${\mathcal{X}}$
.
${\mathcal{X}}$
. -
(ii) Let
 $H\subseteq G$
be a subgroup, whose action on
$H\subseteq G$
be a subgroup, whose action on
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is trivial (for example, this is the case if
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is trivial (for example, this is the case if
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified and
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified and
 $H\subseteq I_{G}$
). Then the
$H\subseteq I_{G}$
). Then the
 $H$
-action on
$H$
-action on
 $X_{L}$
extends to
$X_{L}$
extends to
 ${\mathcal{X}}$
.
${\mathcal{X}}$
.
We first introduce cycle class maps in the context of algebraic spaces.
Lemma 5.6. Let
![]() ${\mathcal{X}}$
be a proper and smooth algebraic space over the spectrum
${\mathcal{X}}$
be a proper and smooth algebraic space over the spectrum
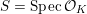 $S=\operatorname{Spec}{\mathcal{O}}_{K}$
of a strictly Henselian DVR
$S=\operatorname{Spec}{\mathcal{O}}_{K}$
of a strictly Henselian DVR
![]() ${\mathcal{O}}_{K}$
, and let
${\mathcal{O}}_{K}$
, and let
![]() ${\mathcal{Z}}\subset {\mathcal{X}}$
be a closed subspace of codimension
${\mathcal{Z}}\subset {\mathcal{X}}$
be a closed subspace of codimension
![]() $c$
that is flat over
$c$
that is flat over
![]() $S$
. Then the natural isomorphism
$S$
. Then the natural isomorphism
 $$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{2c}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Z}/n\mathbb{Z}(c))\rightarrow H_{\acute{\text{e}}\text{t}}^{2c}({\mathcal{X}}_{\overline{K}},\mathbb{Z}/n\mathbb{Z}(c))\end{eqnarray}$$
$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{2c}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Z}/n\mathbb{Z}(c))\rightarrow H_{\acute{\text{e}}\text{t}}^{2c}({\mathcal{X}}_{\overline{K}},\mathbb{Z}/n\mathbb{Z}(c))\end{eqnarray}$$
maps
![]() $[{\mathcal{Z}}_{0}]$
to
$[{\mathcal{Z}}_{0}]$
to
![]() $[{\mathcal{Z}}_{K}]$
.
$[{\mathcal{Z}}_{K}]$
.
Proof. This is immediate if we define a cycle class
![]() $[{\mathcal{Z}}]$
in
$[{\mathcal{Z}}]$
in
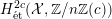 $H_{\acute{\text{e}}\text{t}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))$
in such a way, that it is compatible with base change
$H_{\acute{\text{e}}\text{t}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))$
in such a way, that it is compatible with base change
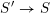 $S^{\prime }\rightarrow S$
of base schemes (and thus, in particular, compatible with restrictions to generic and special fibers). If
$S^{\prime }\rightarrow S$
of base schemes (and thus, in particular, compatible with restrictions to generic and special fibers). If
![]() ${\mathcal{X}}$
is a scheme, this is defined and shown in [Reference DeligneSGA4½, Cycle, Numéro 2.3], and thus it remains to treat the case where
${\mathcal{X}}$
is a scheme, this is defined and shown in [Reference DeligneSGA4½, Cycle, Numéro 2.3], and thus it remains to treat the case where
![]() ${\mathcal{X}}$
is an algebraic space.
${\mathcal{X}}$
is an algebraic space.
First, let us recall cohomological descent. Let
![]() $V\rightarrow {\mathcal{Y}}$
be an étale covering of schemes. Such a morphism is of cohomological descent by [Reference GrothendieckSGA4, Proposition Vbis.4.3.3], and we have a spectral sequence [Reference GrothendieckSGA4, Proposition Vbis.2.5.5]
$V\rightarrow {\mathcal{Y}}$
be an étale covering of schemes. Such a morphism is of cohomological descent by [Reference GrothendieckSGA4, Proposition Vbis.4.3.3], and we have a spectral sequence [Reference GrothendieckSGA4, Proposition Vbis.2.5.5]
 $$\begin{eqnarray}E_{1}^{p,q}:=H_{\acute{\text{e}}\text{t}}^{q}(V_{p},a_{p}^{\ast }F)\Rightarrow H_{\acute{\text{e}}\text{t}}^{p+q}({\mathcal{Y}},F),\end{eqnarray}$$
$$\begin{eqnarray}E_{1}^{p,q}:=H_{\acute{\text{e}}\text{t}}^{q}(V_{p},a_{p}^{\ast }F)\Rightarrow H_{\acute{\text{e}}\text{t}}^{p+q}({\mathcal{Y}},F),\end{eqnarray}$$
where, for each
![]() $p\geqslant 0$
,
$p\geqslant 0$
,
![]() $V_{p}$
is the
$V_{p}$
is the
![]() $(p+1)$
-fold fibered product of
$(p+1)$
-fold fibered product of
![]() $V$
over
$V$
over
![]() ${\mathcal{Y}}$
, and where
${\mathcal{Y}}$
, and where
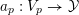 $a_{p}:V_{p}\rightarrow {\mathcal{Y}}$
is the structure map. Next, we consider the more general case, where
$a_{p}:V_{p}\rightarrow {\mathcal{Y}}$
is the structure map. Next, we consider the more general case, where
![]() $V\rightarrow {\mathcal{Y}}$
is an étale covering of an algebraic space by a scheme. (Note that, then, the
$V\rightarrow {\mathcal{Y}}$
is an étale covering of an algebraic space by a scheme. (Note that, then, the
![]() $V_{p}$
are schemes.) We observe that
$V_{p}$
are schemes.) We observe that
![]() $V\rightarrow {\mathcal{Y}}$
is still of cohomological descent (proved in the same way) and we obtain the same spectral sequence.
$V\rightarrow {\mathcal{Y}}$
is still of cohomological descent (proved in the same way) and we obtain the same spectral sequence.
After these preliminary remarks, let
![]() $U\rightarrow {\mathcal{X}}$
be an étale covering by a scheme
$U\rightarrow {\mathcal{X}}$
be an étale covering by a scheme
![]() $U$
. Applying the previous paragraph to the covering
$U$
. Applying the previous paragraph to the covering
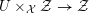 $U\times _{{\mathcal{X}}}{\mathcal{Z}}\rightarrow {\mathcal{Z}}$
and the sheaf
$U\times _{{\mathcal{X}}}{\mathcal{Z}}\rightarrow {\mathcal{Z}}$
and the sheaf
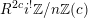 $R^{2c}i^{!}\mathbb{Z}/n\mathbb{Z}(c)$
on
$R^{2c}i^{!}\mathbb{Z}/n\mathbb{Z}(c)$
on
![]() ${\mathcal{Z}}$
(where
${\mathcal{Z}}$
(where
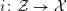 $i:{\mathcal{Z}}\rightarrow {\mathcal{X}}$
is the closed immersion), and using the isomorphism
$i:{\mathcal{Z}}\rightarrow {\mathcal{X}}$
is the closed immersion), and using the isomorphism
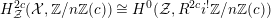 $H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))\cong H^{0}({\mathcal{Z}},R^{2c}i^{!}\mathbb{Z}/n\mathbb{Z}(c))$
(this isomorphism is also proved by reducing to the scheme case), we obtain an isomorphism
$H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))\cong H^{0}({\mathcal{Z}},R^{2c}i^{!}\mathbb{Z}/n\mathbb{Z}(c))$
(this isomorphism is also proved by reducing to the scheme case), we obtain an isomorphism
 $$\begin{eqnarray}\operatorname{Ker}(H_{Z_{0}}^{2c}(U_{0},\mathbb{Z}/n\mathbb{Z}(c))\rightarrow H_{Z_{1}}^{2c}(U_{1},\mathbb{Z}/n\mathbb{Z}(c)))\cong H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c)),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ker}(H_{Z_{0}}^{2c}(U_{0},\mathbb{Z}/n\mathbb{Z}(c))\rightarrow H_{Z_{1}}^{2c}(U_{1},\mathbb{Z}/n\mathbb{Z}(c)))\cong H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c)),\end{eqnarray}$$
where
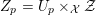 $Z_{p}=U_{p}\times _{{\mathcal{X}}}{\mathcal{Z}}$
(note that this is a scheme). We define
$Z_{p}=U_{p}\times _{{\mathcal{X}}}{\mathcal{Z}}$
(note that this is a scheme). We define
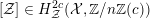 $[{\mathcal{Z}}]\in H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))$
to be
$[{\mathcal{Z}}]\in H_{{\mathcal{Z}}}^{2c}({\mathcal{X}},\mathbb{Z}/n\mathbb{Z}(c))$
to be
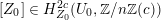 $[Z_{0}]\in H_{Z_{0}}^{2c}(U_{0},\mathbb{Z}/n\mathbb{Z}(c))$
(this class lies indeed in the kernel). Since the cycle map (for schemes) is étale local, this construction does not depend on the choice of the étale covering
$[Z_{0}]\in H_{Z_{0}}^{2c}(U_{0},\mathbb{Z}/n\mathbb{Z}(c))$
(this class lies indeed in the kernel). Since the cycle map (for schemes) is étale local, this construction does not depend on the choice of the étale covering
![]() $U\rightarrow {\mathcal{X}}$
.
$U\rightarrow {\mathcal{X}}$
.
Compatibility with change of base schemes reduces to the scheme case. ◻
Proof of Proposition 5.5.
(i) It follows from the assumptions that
![]() ${\mathcal{X}}_{0}$
is a smooth and proper surface with numerically trivial
${\mathcal{X}}_{0}$
is a smooth and proper surface with numerically trivial
![]() $\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
, and that it has the same
$\unicode[STIX]{x1D714}_{{\mathcal{X}}_{0}/k}$
, and that it has the same
![]() $\ell$
-adic Betti numbers as
$\ell$
-adic Betti numbers as
![]() $X$
. Thus, by the classification of surfaces (see, for example, [Reference Bombieri and MumfordBM77, Theorem 6 and the following Proposition]), also
$X$
. Thus, by the classification of surfaces (see, for example, [Reference Bombieri and MumfordBM77, Theorem 6 and the following Proposition]), also
![]() ${\mathcal{X}}_{0}$
is Abelian and (quasi-)hyperelliptic, respectively. As seen in the proof of Proposition 5.1, the (geometric) exceptional locus of
${\mathcal{X}}_{0}$
is Abelian and (quasi-)hyperelliptic, respectively. As seen in the proof of Proposition 5.1, the (geometric) exceptional locus of
![]() $\unicode[STIX]{x1D70B}$
is a union of
$\unicode[STIX]{x1D70B}$
is a union of
![]() $\mathbb{P}^{1}$
’s with self-intersection number
$\mathbb{P}^{1}$
’s with self-intersection number
![]() $(-2)$
. Now, there are no rational curves on Abelian varieties. Also, it follows from the explicit classification and description of (quasi-)hyperelliptic surfaces in [Reference Bombieri and MumfordBM77, Proposition 5] that they do not contain any smooth rational curves. In particular,
$(-2)$
. Now, there are no rational curves on Abelian varieties. Also, it follows from the explicit classification and description of (quasi-)hyperelliptic surfaces in [Reference Bombieri and MumfordBM77, Proposition 5] that they do not contain any smooth rational curves. In particular,
![]() $\unicode[STIX]{x1D70B}$
must be an isomorphism, which implies that the
$\unicode[STIX]{x1D70B}$
must be an isomorphism, which implies that the
![]() $G$
-action extends to
$G$
-action extends to
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
(ii) After replacing
![]() $K$
by an intermediate extension, we may assume
$K$
by an intermediate extension, we may assume
![]() $H=G$
. To show that the
$H=G$
. To show that the
![]() $G$
-action extends, it suffices to show that the
$G$
-action extends, it suffices to show that the
![]() $\unicode[STIX]{x1D70E}$
-action extends for every
$\unicode[STIX]{x1D70E}$
-action extends for every
![]() $\unicode[STIX]{x1D70E}\in G$
. Thus let
$\unicode[STIX]{x1D70E}\in G$
. Thus let
![]() $\unicode[STIX]{x1D70E}\in G$
, and after replacing
$\unicode[STIX]{x1D70E}\in G$
, and after replacing
![]() $G$
by the cyclic subgroup generated by
$G$
by the cyclic subgroup generated by
![]() $\unicode[STIX]{x1D70E}$
, we may assume that
$\unicode[STIX]{x1D70E}$
, we may assume that
![]() $G$
is cyclic, say
$G$
is cyclic, say
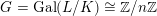 $G=\operatorname{Gal}(L/K)\cong \mathbb{Z}/n\mathbb{Z}$
, and generated by
$G=\operatorname{Gal}(L/K)\cong \mathbb{Z}/n\mathbb{Z}$
, and generated by
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Let
![]() $U\subset {\mathcal{X}}$
be the maximal open subspace to which the
$U\subset {\mathcal{X}}$
be the maximal open subspace to which the
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
extends. Then, as in the proof of Proposition 5.1,
$X_{L}$
extends. Then, as in the proof of Proposition 5.1,
![]() $U$
contains the generic fiber
$U$
contains the generic fiber
![]() $X_{L}$
, as well as an open dense subscheme of the special fiber
$X_{L}$
, as well as an open dense subscheme of the special fiber
![]() ${\mathcal{X}}_{0}$
. Let
${\mathcal{X}}_{0}$
. Let
 $\unicode[STIX]{x1D6E4}\subset {\mathcal{X}}^{n}$
be the closure of the set
$\unicode[STIX]{x1D6E4}\subset {\mathcal{X}}^{n}$
be the closure of the set
 $\{(x,\unicode[STIX]{x1D70E}(x),\ldots ,\unicode[STIX]{x1D70E}^{n-1}(x))\mid x\in U\}$
in
$\{(x,\unicode[STIX]{x1D70E}(x),\ldots ,\unicode[STIX]{x1D70E}^{n-1}(x))\mid x\in U\}$
in
![]() ${\mathcal{X}}^{n}$
. The group
${\mathcal{X}}^{n}$
. The group
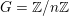 $G=\mathbb{Z}/n\mathbb{Z}$
acts on
$G=\mathbb{Z}/n\mathbb{Z}$
acts on
![]() ${\mathcal{X}}^{n}$
by permutation of the factors, and this action restricted to
${\mathcal{X}}^{n}$
by permutation of the factors, and this action restricted to
![]() $\unicode[STIX]{x1D6E4}_{L}$
coincides with the natural
$\unicode[STIX]{x1D6E4}_{L}$
coincides with the natural
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
via
$X_{L}$
via
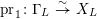 $\operatorname{pr}_{1}:\unicode[STIX]{x1D6E4}_{L}\stackrel{{\sim}}{\rightarrow }X_{L}$
.
$\operatorname{pr}_{1}:\unicode[STIX]{x1D6E4}_{L}\stackrel{{\sim}}{\rightarrow }X_{L}$
.
Consider the diagram of
![]() $G$
-representations
$G$
-representations
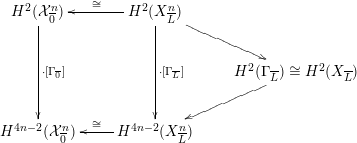
where we omit the coefficients (Tate twists of
![]() $\mathbb{Q}_{\ell }$
) of the
$\mathbb{Q}_{\ell }$
) of the
![]() $\ell$
-adic cohomology groups from the notation, and we write
$\ell$
-adic cohomology groups from the notation, and we write
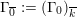 $\unicode[STIX]{x1D6E4}_{\overline{0}}:=(\unicode[STIX]{x1D6E4}_{0})_{\overline{k}}$
and so on. The triangle on the right is clearly commutative. The commutativity of the square on the left follows from the fact that the classes
$\unicode[STIX]{x1D6E4}_{\overline{0}}:=(\unicode[STIX]{x1D6E4}_{0})_{\overline{k}}$
and so on. The triangle on the right is clearly commutative. The commutativity of the square on the left follows from the fact that the classes
![]() $[\unicode[STIX]{x1D6E4}_{\overline{0}}]$
and
$[\unicode[STIX]{x1D6E4}_{\overline{0}}]$
and
![]() $[\unicode[STIX]{x1D6E4}_{\overline{L}}]$
correspond via the isomorphism
$[\unicode[STIX]{x1D6E4}_{\overline{L}}]$
correspond via the isomorphism
 $H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n})\cong H^{4n-4}(X_{\overline{L}}^{n})$
, as proved in Lemma 5.6. Note that all irreducible components of
$H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n})\cong H^{4n-4}(X_{\overline{L}}^{n})$
, as proved in Lemma 5.6. Note that all irreducible components of
![]() $\unicode[STIX]{x1D6E4}_{\overline{0}}$
are of dimension
$\unicode[STIX]{x1D6E4}_{\overline{0}}$
are of dimension
![]() $2$
(by, for example, [Reference LiuLiu02, Proposition 4.4.16]).
$2$
(by, for example, [Reference LiuLiu02, Proposition 4.4.16]).
Let
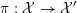 $\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
be as in Proposition 5.1. Let
$\unicode[STIX]{x1D70B}:{\mathcal{X}}\rightarrow {\mathcal{X}}^{\prime }$
be as in Proposition 5.1. Let
![]() $E\subset {\mathcal{X}}_{0}$
be the exceptional locus of
$E\subset {\mathcal{X}}_{0}$
be the exceptional locus of
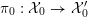 $\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
and
$\unicode[STIX]{x1D70B}_{0}:{\mathcal{X}}_{0}\rightarrow {\mathcal{X}}_{0}^{\prime }$
and
![]() $E^{\unicode[STIX]{x1D6FC}}$
be the irreducible components of
$E^{\unicode[STIX]{x1D6FC}}$
be the irreducible components of
![]() $E_{\overline{k}}$
. Each irreducible component
$E_{\overline{k}}$
. Each irreducible component
![]() $E^{\unicode[STIX]{x1D6FC}}$
is isomorphic to
$E^{\unicode[STIX]{x1D6FC}}$
is isomorphic to
![]() $\mathbb{P}^{1}$
. Since
$\mathbb{P}^{1}$
. Since
![]() $\unicode[STIX]{x1D70B}_{0}$
is a resolution of singularities, the intersection matrix
$\unicode[STIX]{x1D70B}_{0}$
is a resolution of singularities, the intersection matrix
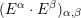 $(E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}})_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
is negative definite (by Hodge index theorem), hence invertible. In particular, if we are given
$(E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}})_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
is negative definite (by Hodge index theorem), hence invertible. In particular, if we are given
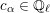 $c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Q}_{\ell }$
for
$c_{\unicode[STIX]{x1D6FC}}\in \mathbb{Q}_{\ell }$
for
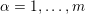 $\unicode[STIX]{x1D6FC}=1,\ldots ,m$
, such that
$\unicode[STIX]{x1D6FC}=1,\ldots ,m$
, such that
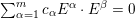 $\sum _{\unicode[STIX]{x1D6FC}=1}^{m}c_{\unicode[STIX]{x1D6FC}}E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}}=0$
for all
$\sum _{\unicode[STIX]{x1D6FC}=1}^{m}c_{\unicode[STIX]{x1D6FC}}E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}}=0$
for all
![]() $\unicode[STIX]{x1D6FD}$
, then
$\unicode[STIX]{x1D6FD}$
, then
![]() $c_{\unicode[STIX]{x1D6FC}}=0$
for all
$c_{\unicode[STIX]{x1D6FC}}=0$
for all
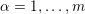 $\unicode[STIX]{x1D6FC}=1,\ldots ,m$
.
$\unicode[STIX]{x1D6FC}=1,\ldots ,m$
.
Consider the irreducible components of
![]() $\unicode[STIX]{x1D6E4}_{\overline{0}}$
. First, there is the ‘diagonal’ component, that is, the closure of the set
$\unicode[STIX]{x1D6E4}_{\overline{0}}$
. First, there is the ‘diagonal’ component, that is, the closure of the set
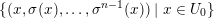 $\{(x,\unicode[STIX]{x1D70E}(x),\ldots ,\unicode[STIX]{x1D70E}^{n-1}(x))\mid x\in U_{0}\}$
. If
$\{(x,\unicode[STIX]{x1D70E}(x),\ldots ,\unicode[STIX]{x1D70E}^{n-1}(x))\mid x\in U_{0}\}$
. If
![]() $Z$
is a non-diagonal component (assuming there is one), then
$Z$
is a non-diagonal component (assuming there is one), then
![]() $Z$
is contained in
$Z$
is contained in
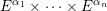 $E^{\unicode[STIX]{x1D6FC}_{1}}\times \cdots \times E^{\unicode[STIX]{x1D6FC}_{n}}$
for some
$E^{\unicode[STIX]{x1D6FC}_{1}}\times \cdots \times E^{\unicode[STIX]{x1D6FC}_{n}}$
for some
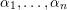 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
. From the Künneth formula and the fact that
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
. From the Künneth formula and the fact that
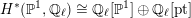 $H^{\ast }(\mathbb{P}^{1},\mathbb{Q}_{\ell })\cong \mathbb{Q}_{\ell }[\mathbb{P}^{1}]\oplus \mathbb{Q}_{\ell }[\operatorname{pt}]$
, it follows that the cycle class
$H^{\ast }(\mathbb{P}^{1},\mathbb{Q}_{\ell })\cong \mathbb{Q}_{\ell }[\mathbb{P}^{1}]\oplus \mathbb{Q}_{\ell }[\operatorname{pt}]$
, it follows that the cycle class
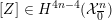 $[Z]\in H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n})$
is a non-zero
$[Z]\in H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n})$
is a non-zero
![]() $\mathbb{Z}_{{\geqslant}0}$
-combination of
$\mathbb{Z}_{{\geqslant}0}$
-combination of
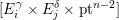 $[E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}]$
with
$[E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}]$
with
![]() $i\neq j$
, where
$i\neq j$
, where
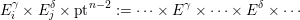 $$\begin{eqnarray}E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}:=\cdots \times E^{\unicode[STIX]{x1D6FE}}\times \cdots \times E^{\unicode[STIX]{x1D6FF}}\times \cdots\end{eqnarray}$$
$$\begin{eqnarray}E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}:=\cdots \times E^{\unicode[STIX]{x1D6FE}}\times \cdots \times E^{\unicode[STIX]{x1D6FF}}\times \cdots\end{eqnarray}$$
(the
![]() $i$
th component is equal to
$i$
th component is equal to
![]() $E^{\unicode[STIX]{x1D6FE}}$
, the
$E^{\unicode[STIX]{x1D6FE}}$
, the
![]() $j$
th component is equal to
$j$
th component is equal to
![]() $E^{\unicode[STIX]{x1D6FF}}$
, and the remaining components are equal to a point). Hence, if we set
$E^{\unicode[STIX]{x1D6FF}}$
, and the remaining components are equal to a point). Hence, if we set
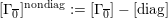 $[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}:=[\unicode[STIX]{x1D6E4}_{\overline{0}}]-[\operatorname{diag}]$
, then there exist
$[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}:=[\unicode[STIX]{x1D6E4}_{\overline{0}}]-[\operatorname{diag}]$
, then there exist
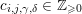 $c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}\in \mathbb{Z}_{{\geqslant}0}$
such that
$c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}\in \mathbb{Z}_{{\geqslant}0}$
such that
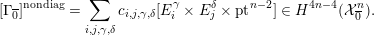 $$\begin{eqnarray}[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=\mathop{\sum }_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}[E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}]\in H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n}).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=\mathop{\sum }_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}[E_{i}^{\unicode[STIX]{x1D6FE}}\times E_{j}^{\unicode[STIX]{x1D6FF}}\times \operatorname{pt}^{n-2}]\in H^{4n-4}({\mathcal{X}}_{\overline{0}}^{n}).\end{eqnarray}$$
We have
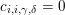 $c_{i,i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}=0$
for all
$c_{i,i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}=0$
for all
![]() $i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
.
$i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
.
We want to show
 $[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=0$
. For this, we will use the assumption that the
$[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=0$
. For this, we will use the assumption that the
![]() $G$
-action on
$G$
-action on
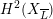 $H^{2}(X_{\overline{L}})$
is trivial. Using the commutative diagram (3), we see that the map
$H^{2}(X_{\overline{L}})$
is trivial. Using the commutative diagram (3), we see that the map
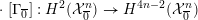 $\cdot \,\,[\unicode[STIX]{x1D6E4}_{\overline{0}}]:H^{2}({\mathcal{X}}_{\overline{0}}^{n})\rightarrow H^{4n-2}({\mathcal{X}}_{\overline{0}}^{n})$
factors through
$\cdot \,\,[\unicode[STIX]{x1D6E4}_{\overline{0}}]:H^{2}({\mathcal{X}}_{\overline{0}}^{n})\rightarrow H^{4n-2}({\mathcal{X}}_{\overline{0}}^{n})$
factors through
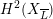 $H^{2}(X_{\overline{L}})$
, and thus every element in its image is
$H^{2}(X_{\overline{L}})$
, and thus every element in its image is
![]() $G$
-invariant. In particular, for all
$G$
-invariant. In particular, for all
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $i$
, the cycle
$i$
, the cycle
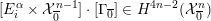 $[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]\in H^{4n-2}({\mathcal{X}}_{\overline{0}}^{n})$
is
$[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]\in H^{4n-2}({\mathcal{X}}_{\overline{0}}^{n})$
is
![]() $G$
-invariant, where
$G$
-invariant, where
 $$\begin{eqnarray}E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}:=\cdots \times E^{\unicode[STIX]{x1D6FC}}\times \cdots\end{eqnarray}$$
$$\begin{eqnarray}E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}:=\cdots \times E^{\unicode[STIX]{x1D6FC}}\times \cdots\end{eqnarray}$$
(the
![]() $i$
th component is equal to
$i$
th component is equal to
![]() $E^{\unicode[STIX]{x1D6FC}}$
and the remaining components are equal to
$E^{\unicode[STIX]{x1D6FC}}$
and the remaining components are equal to
![]() ${\mathcal{X}}_{\overline{0}}$
). Now,
${\mathcal{X}}_{\overline{0}}$
). Now,
![]() $G$
acts by
$G$
acts by
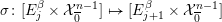 $\unicode[STIX]{x1D70E}:[E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\mapsto [E_{j+1}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
, which implies that for all
$\unicode[STIX]{x1D70E}:[E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\mapsto [E_{j+1}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
, which implies that for all
![]() $\unicode[STIX]{x1D6FD}$
, the cycle
$\unicode[STIX]{x1D6FD}$
, the cycle
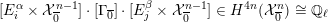 $[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\in H^{4n}({\mathcal{X}}_{\overline{0}}^{n})\cong \mathbb{Q}_{\ell }$
is independent of
$[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\in H^{4n}({\mathcal{X}}_{\overline{0}}^{n})\cong \mathbb{Q}_{\ell }$
is independent of
![]() $j$
. Since
$j$
. Since
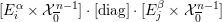 $[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\operatorname{diag}]\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
is equal to
$[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\operatorname{diag}]\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
is equal to
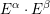 $E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}}$
, it is also independent of
$E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}}$
, it is also independent of
![]() $j$
, and thus
$j$
, and thus
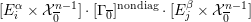 $[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
is independent of
$[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]$
is independent of
![]() $j$
for all
$j$
for all
![]() $\unicode[STIX]{x1D6FD}$
. In order to compute its value, we use (4) and find
$\unicode[STIX]{x1D6FD}$
. In order to compute its value, we use (4) and find
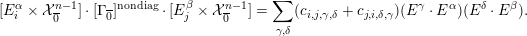 $$\begin{eqnarray}[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]=\mathop{\sum }_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}(c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}+c_{j,i,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}})(E^{\unicode[STIX]{x1D6FE}}\cdot E^{\unicode[STIX]{x1D6FC}})(E^{\unicode[STIX]{x1D6FF}}\cdot E^{\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
$$\begin{eqnarray}[E_{i}^{\unicode[STIX]{x1D6FC}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]\cdot [\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}\cdot [E_{j}^{\unicode[STIX]{x1D6FD}}\times {\mathcal{X}}_{\overline{0}}^{n-1}]=\mathop{\sum }_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}(c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}+c_{j,i,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}})(E^{\unicode[STIX]{x1D6FE}}\cdot E^{\unicode[STIX]{x1D6FC}})(E^{\unicode[STIX]{x1D6FF}}\cdot E^{\unicode[STIX]{x1D6FD}}).\end{eqnarray}$$
Since
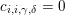 $c_{i,i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}=0$
for all
$c_{i,i,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}=0$
for all
![]() $i$
, this sum is zero for
$i$
, this sum is zero for
![]() $i=j$
. Since it is independent of
$i=j$
. Since it is independent of
![]() $j$
, this sum is zero for all
$j$
, this sum is zero for all
![]() $i,j$
. Using invertibility of the matrix
$i,j$
. Using invertibility of the matrix
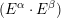 $(E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}})$
twice, we obtain
$(E^{\unicode[STIX]{x1D6FC}}\cdot E^{\unicode[STIX]{x1D6FD}})$
twice, we obtain
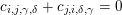 $c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}+c_{j,i,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}=0$
for all
$c_{i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}}+c_{j,i,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}=0$
for all
![]() $i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
. Thus
$i,j,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
. Thus
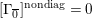 $[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=0$
.
$[\unicode[STIX]{x1D6E4}_{\overline{0}}]^{\text{nondiag}}=0$
.
Now,
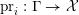 $\operatorname{pr}_{i}:\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{X}}$
is a proper birational morphism for all
$\operatorname{pr}_{i}:\unicode[STIX]{x1D6E4}\rightarrow {\mathcal{X}}$
is a proper birational morphism for all
![]() $i$
, where
$i$
, where
![]() ${\mathcal{X}}$
is regular, and
${\mathcal{X}}$
is regular, and
![]() $\unicode[STIX]{x1D6E4}$
is integral. Thus, by van der Waerden purity (see, [Reference LiuLiu02, Theorem 7.2.22], for example, and note that this result can easily be extended to algebraic spaces), the exceptional locus of
$\unicode[STIX]{x1D6E4}$
is integral. Thus, by van der Waerden purity (see, [Reference LiuLiu02, Theorem 7.2.22], for example, and note that this result can easily be extended to algebraic spaces), the exceptional locus of
![]() $\operatorname{pr}_{i}$
is either empty or a divisor. If it was a divisor, it would give rise to a non-diagonal component of
$\operatorname{pr}_{i}$
is either empty or a divisor. If it was a divisor, it would give rise to a non-diagonal component of
![]() $\unicode[STIX]{x1D6E4}_{\overline{0}}$
, which does not exist by the previous computations. Thus
$\unicode[STIX]{x1D6E4}_{\overline{0}}$
, which does not exist by the previous computations. Thus
![]() $\operatorname{pr}_{i}$
is an isomorphism for all
$\operatorname{pr}_{i}$
is an isomorphism for all
![]() $i$
, and since the
$i$
, and since the
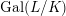 $\operatorname{Gal}(L/K)$
-action extends to
$\operatorname{Gal}(L/K)$
-action extends to
![]() $\unicode[STIX]{x1D6E4}$
, this shows that the
$\unicode[STIX]{x1D6E4}$
, this shows that the
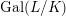 $\operatorname{Gal}(L/K)$
-action extends to
$\operatorname{Gal}(L/K)$
-action extends to
![]() ${\mathcal{X}}$
, as desired.◻
${\mathcal{X}}$
, as desired.◻
Remark 5.7. We stress that the reason for the extension of the
![]() $G$
-action to
$G$
-action to
![]() ${\mathcal{X}}$
rather than
${\mathcal{X}}$
rather than
![]() ${\mathcal{X}}^{\prime }$
in the case of Abelian and hyperelliptic surfaces is their ‘simple’ geometry: they contain no smooth rational curves.
${\mathcal{X}}^{\prime }$
in the case of Abelian and hyperelliptic surfaces is their ‘simple’ geometry: they contain no smooth rational curves.
5.4 The action on the special fiber
In the situation of Proposition 5.5, we now want to understand whether the induced
![]() $G$
-action on the special fiber
$G$
-action on the special fiber
![]() ${\mathcal{X}}_{0}$
is trivial. Quite generally, if
${\mathcal{X}}_{0}$
is trivial. Quite generally, if
![]() $Y$
is a smooth and proper variety over some field
$Y$
is a smooth and proper variety over some field
![]() $k$
, then the natural representation
$k$
, then the natural representation
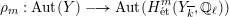 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{m}:\operatorname{Aut}(Y)\longrightarrow \operatorname{Aut}(H_{\acute{\text{e}}\text{t}}^{m}(Y_{\overline{k}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{m}:\operatorname{Aut}(Y)\longrightarrow \operatorname{Aut}(H_{\acute{\text{e}}\text{t}}^{m}(Y_{\overline{k}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
is usually neither injective nor surjective. We have the following exceptions.
-
(i) If
 $Y$
is an Abelian variety, then
$Y$
is an Abelian variety, then
 $\unicode[STIX]{x1D70C}_{1}$
is injective. (Here,
$\unicode[STIX]{x1D70C}_{1}$
is injective. (Here,
 $\operatorname{Aut}(Y)$
denotes the automorphism group as an Abelian variety – translations may act trivially on cohomology.)
$\operatorname{Aut}(Y)$
denotes the automorphism group as an Abelian variety – translations may act trivially on cohomology.) -
(ii) If
 $Y$
is a K3 surface, then
$Y$
is a K3 surface, then
 $\unicode[STIX]{x1D70C}_{2}$
is injective.
$\unicode[STIX]{x1D70C}_{2}$
is injective.
Using these results (for references, see below), we have the following.
Proposition 5.8. We keep the notation and assumptions of Proposition 5.1. Moreover, assume that either:
-
(i)
 $X$
is an Abelian surface and the
$X$
is an Abelian surface and the
 $G$
-action on
$G$
-action on
 $H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified; or
$H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified; or -
(ii)
 $X$
is a K3 surface and the
$X$
is a K3 surface and the
 $G$
-action on
$G$
-action on
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified.
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified.
Then the
![]() $I_{G}$
-action on
$I_{G}$
-action on
![]() $X_{L}$
extends to
$X_{L}$
extends to
![]() ${\mathcal{X}}$
, and the induced
${\mathcal{X}}$
, and the induced
![]() $I_{G}$
-action on the special fiber
$I_{G}$
-action on the special fiber
![]() ${\mathcal{X}}_{0}$
is trivial.
${\mathcal{X}}_{0}$
is trivial.
Proof. We have already shown the extension of the
![]() $I_{G}$
-action to
$I_{G}$
-action to
![]() ${\mathcal{X}}$
in Proposition 5.5. Moreover, the
${\mathcal{X}}$
in Proposition 5.5. Moreover, the
![]() $I_{G}$
-action on
$I_{G}$
-action on
![]() ${\mathcal{X}}_{0}$
is
${\mathcal{X}}_{0}$
is
![]() $k$
-linear. By assumption, the
$k$
-linear. By assumption, the
![]() $I_{G}$
-action on
$I_{G}$
-action on
 $H_{\acute{\text{e}}\text{t}}^{m}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })$
is trivial for
$H_{\acute{\text{e}}\text{t}}^{m}(({\mathcal{X}}_{0})_{\overline{k}},\mathbb{Q}_{\ell })$
is trivial for
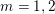 $m=1,2$
, respectively.
$m=1,2$
, respectively.
If
![]() $X$
is an Abelian surface, then the
$X$
is an Abelian surface, then the
![]() $I_{G}$
-action on
$I_{G}$
-action on
![]() $({\mathcal{X}}_{0})_{\overline{k}}$
is trivial by the injectivity of
$({\mathcal{X}}_{0})_{\overline{k}}$
is trivial by the injectivity of
![]() $\unicode[STIX]{x1D70C}_{1}$
in arbitrary characteristic; see, for example, [Reference MumfordMum70, Theorem 3 in §19]. If
$\unicode[STIX]{x1D70C}_{1}$
in arbitrary characteristic; see, for example, [Reference MumfordMum70, Theorem 3 in §19]. If
![]() $X$
is a K3 surface, then the
$X$
is a K3 surface, then the
![]() $I_{G}$
-action on
$I_{G}$
-action on
![]() $({\mathcal{X}}_{0})_{\overline{k}}$
is trivial by the injectivity of
$({\mathcal{X}}_{0})_{\overline{k}}$
is trivial by the injectivity of
![]() $\unicode[STIX]{x1D70C}_{2}$
in arbitrary characteristic; see [Reference OgusOgu79, Corollary 2.5] and [Reference KeumKeu16, Theorem 1.4] (in the case of complex and possibly non-algebraic K3 surfaces, see [Reference BeauvilleBea85, Proposition IX.6] and [Reference HuybrechtsHuy16, Proposition 15.2.1]). In both cases, the
$\unicode[STIX]{x1D70C}_{2}$
in arbitrary characteristic; see [Reference OgusOgu79, Corollary 2.5] and [Reference KeumKeu16, Theorem 1.4] (in the case of complex and possibly non-algebraic K3 surfaces, see [Reference BeauvilleBea85, Proposition IX.6] and [Reference HuybrechtsHuy16, Proposition 15.2.1]). In both cases, the
![]() $I_{G}$
-action on
$I_{G}$
-action on
![]() $({\mathcal{X}}_{0})_{\overline{k}}$
is trivial, and thus also the original action on
$({\mathcal{X}}_{0})_{\overline{k}}$
is trivial, and thus also the original action on
![]() ${\mathcal{X}}_{0}$
is trivial.◻
${\mathcal{X}}_{0}$
is trivial.◻
5.5 Tame quotients
Now, in the situation of Proposition 5.5, it is natural to study the quotient
![]() ${\mathcal{X}}/H$
and its special fiber, where
${\mathcal{X}}/H$
and its special fiber, where
![]() $H$
is a subgroup of
$H$
is a subgroup of
![]() $G$
. We start with the following easy result.
$G$
. We start with the following easy result.
Proposition 5.9. Let
![]() $X$
be a smooth and proper variety over
$X$
be a smooth and proper variety over
![]() $K$
. Let
$K$
. Let
![]() $L/K$
be a finite Galois extension with group
$L/K$
be a finite Galois extension with group
![]() $G$
, such that
$G$
, such that
![]() $X_{L}$
admits a smooth model
$X_{L}$
admits a smooth model
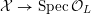 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Moreover, assume that the natural
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Moreover, assume that the natural
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
extends to
$X_{L}$
extends to
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
such that:
$G$
such that:
-
(i)
 $H$
is contained in the inertia subgroup of
$H$
is contained in the inertia subgroup of
 $G$
;
$G$
; -
(ii)
 $H$
is of order prime to
$H$
is of order prime to
 $p$
; and
$p$
; and -
(iii)
 $H$
acts trivially on the special fiber
$H$
acts trivially on the special fiber
 ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
Then:
-
(i) the quotient
 ${\mathcal{X}}/H$
is smooth over
${\mathcal{X}}/H$
is smooth over
 $\operatorname{Spec}{\mathcal{O}}_{L}^{H}$
;
$\operatorname{Spec}{\mathcal{O}}_{L}^{H}$
; -
(ii) the special fiber of
 ${\mathcal{X}}/H$
is isomorphic to
${\mathcal{X}}/H$
is isomorphic to
 ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
Proof. First of all, the quotient
![]() ${\mathcal{X}}/H$
exists in the category of algebraic spaces [Reference KnutsonKnu71, ch. IV.1]. Next, let
${\mathcal{X}}/H$
exists in the category of algebraic spaces [Reference KnutsonKnu71, ch. IV.1]. Next, let
![]() $\widehat{{\mathcal{X}}}_{0}$
be the formal completion of
$\widehat{{\mathcal{X}}}_{0}$
be the formal completion of
![]() ${\mathcal{X}}$
along the special fiber
${\mathcal{X}}$
along the special fiber
![]() ${\mathcal{X}}_{0}$
, which is a formal scheme. If
${\mathcal{X}}_{0}$
, which is a formal scheme. If
![]() $x\in {\mathcal{X}}_{0}$
is a closed point, then
$x\in {\mathcal{X}}_{0}$
is a closed point, then
![]() ${\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
is étale over the localization
${\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
is étale over the localization
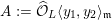 $A:=\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
of the restricted power series ring
$A:=\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
of the restricted power series ring
 $$\begin{eqnarray}\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle :=\biggl\{\mathop{\sum }_{i_{1},i_{2}\geqslant 0}a_{i_{1},i_{2}}y_{1}^{i_{1}}y_{2}^{i_{2}}\in \widehat{{\mathcal{O}}}_{L}[[y_{1},y_{2}]]\biggm\vert\begin{array}{@{}l@{}}\operatorname{ord}_{\unicode[STIX]{x1D70B}}(a_{i_{1},i_{2}})\rightarrow \infty \\ \text{as }i_{1}+i_{2}\rightarrow \infty \end{array}\biggr\}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle :=\biggl\{\mathop{\sum }_{i_{1},i_{2}\geqslant 0}a_{i_{1},i_{2}}y_{1}^{i_{1}}y_{2}^{i_{2}}\in \widehat{{\mathcal{O}}}_{L}[[y_{1},y_{2}]]\biggm\vert\begin{array}{@{}l@{}}\operatorname{ord}_{\unicode[STIX]{x1D70B}}(a_{i_{1},i_{2}})\rightarrow \infty \\ \text{as }i_{1}+i_{2}\rightarrow \infty \end{array}\biggr\}\end{eqnarray}$$
at the maximal ideal
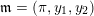 $\mathfrak{m}=(\unicode[STIX]{x1D70B},y_{1},y_{2})$
. The induced
$\mathfrak{m}=(\unicode[STIX]{x1D70B},y_{1},y_{2})$
. The induced
![]() $H$
-action on the residue ring
$H$
-action on the residue ring
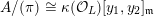 $A/(\unicode[STIX]{x1D70B})\cong \unicode[STIX]{x1D705}({\mathcal{O}}_{L})[y_{1},y_{2}]_{\mathfrak{m}}$
is trivial. Thus replacing
$A/(\unicode[STIX]{x1D70B})\cong \unicode[STIX]{x1D705}({\mathcal{O}}_{L})[y_{1},y_{2}]_{\mathfrak{m}}$
is trivial. Thus replacing
![]() $y_{i}$
by
$y_{i}$
by
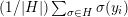 $(1/|H|)\sum _{\unicode[STIX]{x1D70E}\in H}\unicode[STIX]{x1D70E}(y_{i})$
for
$(1/|H|)\sum _{\unicode[STIX]{x1D70E}\in H}\unicode[STIX]{x1D70E}(y_{i})$
for
![]() $i=1,2$
(here, we use that the order of
$i=1,2$
(here, we use that the order of
![]() $H$
is prime to
$H$
is prime to
![]() $p$
) is simply a change of coordinates of
$p$
) is simply a change of coordinates of
![]() $A$
. But then the
$A$
. But then the
![]() $H$
-action on
$H$
-action on
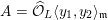 $A=\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
is trivial on
$A=\widehat{{\mathcal{O}}}_{L}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
is trivial on
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
, and hence
$y_{2}$
, and hence
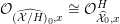 ${\mathcal{O}}_{\widehat{({\mathcal{X}}/H)}_{0},x}\cong {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}^{H}$
is étale over
${\mathcal{O}}_{\widehat{({\mathcal{X}}/H)}_{0},x}\cong {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}^{H}$
is étale over
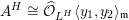 $A^{H}\cong \widehat{{\mathcal{O}}}_{L^{H}}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
. From this local and formal description, the smoothness of
$A^{H}\cong \widehat{{\mathcal{O}}}_{L^{H}}\langle y_{1},y_{2}\rangle _{\mathfrak{m}}$
. From this local and formal description, the smoothness of
![]() ${\mathcal{X}}/H$
follows immediately, and we see that the quotient map
${\mathcal{X}}/H$
follows immediately, and we see that the quotient map
 ${\mathcal{X}}\rightarrow {\mathcal{X}}/H$
induces an isomorphism of special fibers.◻
${\mathcal{X}}\rightarrow {\mathcal{X}}/H$
induces an isomorphism of special fibers.◻
5.6 Wild quotients
Unfortunately, Proposition 5.9 is no longer true if
![]() $p\neq 0$
and
$p\neq 0$
and
![]() $H$
is a subgroup of the inertia subgroup, whose order is divisible by
$H$
is a subgroup of the inertia subgroup, whose order is divisible by
![]() $p$
. Let us illustrate this with a very instructive example. We refer the interested reader to Wewers’ article [Reference WewersWew10] for a more thorough treatment of wild actions and their quotients.
$p$
. Let us illustrate this with a very instructive example. We refer the interested reader to Wewers’ article [Reference WewersWew10] for a more thorough treatment of wild actions and their quotients.
Example 5.10. Consider
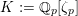 $K:=\mathbb{Q}_{p}[\unicode[STIX]{x1D701}_{p}]$
, where
$K:=\mathbb{Q}_{p}[\unicode[STIX]{x1D701}_{p}]$
, where
![]() $\unicode[STIX]{x1D701}_{p}$
is a primitive
$\unicode[STIX]{x1D701}_{p}$
is a primitive
![]() $p$
th root of unity. Then
$p$
th root of unity. Then
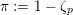 $\unicode[STIX]{x1D70B}:=1-\unicode[STIX]{x1D701}_{p}$
is a uniformizer in
$\unicode[STIX]{x1D70B}:=1-\unicode[STIX]{x1D701}_{p}$
is a uniformizer in
![]() ${\mathcal{O}}_{K}$
, and the residue field is
${\mathcal{O}}_{K}$
, and the residue field is
![]() $\mathbb{F}_{p}$
; see [Reference WashingtonWas82, Lemma 1.4], for example. Let
$\mathbb{F}_{p}$
; see [Reference WashingtonWas82, Lemma 1.4], for example. Let
![]() $L$
be the finite extension
$L$
be the finite extension
![]() $K[\unicode[STIX]{x1D71B}]$
, where
$K[\unicode[STIX]{x1D71B}]$
, where
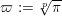 $\unicode[STIX]{x1D71B}:=\sqrt[p]{\unicode[STIX]{x1D70B}}$
. Then
$\unicode[STIX]{x1D71B}:=\sqrt[p]{\unicode[STIX]{x1D70B}}$
. Then
![]() $\unicode[STIX]{x1D71B}$
is a uniformizer in
$\unicode[STIX]{x1D71B}$
is a uniformizer in
![]() ${\mathcal{O}}_{L}$
, and the residue field is
${\mathcal{O}}_{L}$
, and the residue field is
![]() $\mathbb{F}_{p}$
, that is,
$\mathbb{F}_{p}$
, that is,
![]() $L/K$
is totally ramified. By Kummer theory,
$L/K$
is totally ramified. By Kummer theory,
![]() $L/K$
is Galois with group
$L/K$
is Galois with group
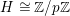 $H\cong \mathbb{Z}/p\mathbb{Z}$
. More precisely, there exists a generator
$H\cong \mathbb{Z}/p\mathbb{Z}$
. More precisely, there exists a generator
![]() $\unicode[STIX]{x1D70E}\in H$
such that
$\unicode[STIX]{x1D70E}\in H$
such that
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B})=\unicode[STIX]{x1D701}_{p}\cdot \unicode[STIX]{x1D71B}$
. We set
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B})=\unicode[STIX]{x1D701}_{p}\cdot \unicode[STIX]{x1D71B}$
. We set
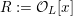 $$\begin{eqnarray}R:={\mathcal{O}}_{L}[x]\end{eqnarray}$$
$$\begin{eqnarray}R:={\mathcal{O}}_{L}[x]\end{eqnarray}$$
and extend the
![]() $H$
-action to
$H$
-action to
![]() $R$
by requiring that
$R$
by requiring that
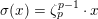 $\unicode[STIX]{x1D70E}(x)=\unicode[STIX]{x1D701}_{p}^{p-1}\cdot x$
. Then we have
$\unicode[STIX]{x1D70E}(x)=\unicode[STIX]{x1D701}_{p}^{p-1}\cdot x$
. Then we have
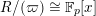 $R/(\unicode[STIX]{x1D71B})\cong \mathbb{F}_{p}[x]$
, and the induced
$R/(\unicode[STIX]{x1D71B})\cong \mathbb{F}_{p}[x]$
, and the induced
![]() $H$
-action on the quotient is trivial. On the other hand, we find that
$H$
-action on the quotient is trivial. On the other hand, we find that
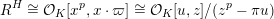 $$\begin{eqnarray}R^{H}\cong {\mathcal{O}}_{K}[x^{p},x\cdot \unicode[STIX]{x1D71B}]\cong {\mathcal{O}}_{K}[u,z]/(z^{p}-\unicode[STIX]{x1D70B}u)\end{eqnarray}$$
$$\begin{eqnarray}R^{H}\cong {\mathcal{O}}_{K}[x^{p},x\cdot \unicode[STIX]{x1D71B}]\cong {\mathcal{O}}_{K}[u,z]/(z^{p}-\unicode[STIX]{x1D70B}u)\end{eqnarray}$$
is normal, but not regular – this is an arithmetic version of the RDP singularity of type
![]() $A_{p-1}$
. We also find that the special fiber
$A_{p-1}$
. We also find that the special fiber
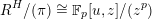 $$\begin{eqnarray}R^{H}/(\unicode[STIX]{x1D70B})\cong \mathbb{F}_{p}[u,z]/(z^{p})\end{eqnarray}$$
$$\begin{eqnarray}R^{H}/(\unicode[STIX]{x1D70B})\cong \mathbb{F}_{p}[u,z]/(z^{p})\end{eqnarray}$$
is not reduced. In particular, Proposition 5.9 does not extend to wild actions without extra assumptions. However, let us make two observations, whose significance will become clear in the proof of Proposition 5.11.
-
(i) The
 $H$
-action on the special fiber
$H$
-action on the special fiber
 $R/(\unicode[STIX]{x1D71B})$
only seems to be trivial, but in fact, it has become infinitesimal. More precisely, if
$R/(\unicode[STIX]{x1D71B})$
only seems to be trivial, but in fact, it has become infinitesimal. More precisely, if
 $r\in R$
and
$r\in R$
and
 $\overline{r}$
denotes its residue class in
$\overline{r}$
denotes its residue class in
 $R/(\unicode[STIX]{x1D71B})$
, then the
$R/(\unicode[STIX]{x1D71B})$
, then the
 $H$
-action gives rise to a well-defined and non-trivial derivation
$H$
-action gives rise to a well-defined and non-trivial derivation  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:R/(\unicode[STIX]{x1D71B}) & \rightarrow & \displaystyle R/(\unicode[STIX]{x1D71B})\nonumber\\ \displaystyle \overline{r} & \mapsto & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70E}(r)-r}{\unicode[STIX]{x1D70B}}\biggr)\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D71B}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:R/(\unicode[STIX]{x1D71B}) & \rightarrow & \displaystyle R/(\unicode[STIX]{x1D71B})\nonumber\\ \displaystyle \overline{r} & \mapsto & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70E}(r)-r}{\unicode[STIX]{x1D70B}}\biggr)\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D71B}.\nonumber\end{eqnarray}$$
-
(ii) The augmentation ideal, that is, the ideal of
 $R$
generated by all elements of the form
$R$
generated by all elements of the form
 $\unicode[STIX]{x1D70E}(r)-r$
, is not principal. In fact, it can be generated by the two elements
$\unicode[STIX]{x1D70E}(r)-r$
, is not principal. In fact, it can be generated by the two elements
 $\unicode[STIX]{x1D71B}^{p}x$
and
$\unicode[STIX]{x1D71B}^{p}x$
and
 $\unicode[STIX]{x1D71B}^{p+1}$
.
$\unicode[STIX]{x1D71B}^{p+1}$
.
Despite this example, we have the following analog of Proposition 5.9 in the wildly ramified case. The main ideas of its proof are due to Király and Lütkebohmert [Reference Király and LütkebohmertKL13, Theorem 2] and Wewers [Reference WewersWew10, Proposition 3.2].
Proposition 5.11. Let
![]() $X$
be a smooth and proper variety over
$X$
be a smooth and proper variety over
![]() $K$
. Let
$K$
. Let
![]() $L/K$
be a finite Galois extension with group
$L/K$
be a finite Galois extension with group
![]() $G$
, such that
$G$
, such that
![]() $X_{L}$
admits a smooth model
$X_{L}$
admits a smooth model
 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Moreover, assume that the natural
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Moreover, assume that the natural
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
extends to
$X_{L}$
extends to
![]() ${\mathcal{X}}$
. Let
${\mathcal{X}}$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
such that:
$G$
such that:
-
(i)
 $H$
is contained in the inertia subgroup of
$H$
is contained in the inertia subgroup of
 $G$
;
$G$
; -
(ii)
 $H$
is cyclic of order
$H$
is cyclic of order
 $p\geqslant 2$
; and
$p\geqslant 2$
; and -
(iii)
 $H$
acts trivially on the special fiber
$H$
acts trivially on the special fiber
 ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
Then the
![]() $H$
-action induces a global and non-trivial derivation on
$H$
-action induces a global and non-trivial derivation on
![]() ${\mathcal{X}}_{0}$
or else both of the following two statements hold true:
${\mathcal{X}}_{0}$
or else both of the following two statements hold true:
-
(i) the quotient
 ${\mathcal{X}}/H$
is smooth over
${\mathcal{X}}/H$
is smooth over
 ${\mathcal{O}}_{L}^{H}$
;
${\mathcal{O}}_{L}^{H}$
; -
(ii) the special fiber of
 ${\mathcal{X}}/H$
is isomorphic to
${\mathcal{X}}/H$
is isomorphic to
 ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
Proof. First of all, the quotient
![]() ${\mathcal{X}}/H$
exists in the category of algebraic spaces [Reference KnutsonKnu71, ch. IV.1]. Next, we fix once and for all a generator
${\mathcal{X}}/H$
exists in the category of algebraic spaces [Reference KnutsonKnu71, ch. IV.1]. Next, we fix once and for all a generator
![]() $\unicode[STIX]{x1D70E}\in H$
and a uniformizer
$\unicode[STIX]{x1D70E}\in H$
and a uniformizer
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{L}$
. We use these to define the following:
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{L}$
. We use these to define the following:
 $$\begin{eqnarray}\displaystyle N({\mathcal{O}}_{L}) & := & \displaystyle \max \{k\mid \unicode[STIX]{x1D70B}^{k}\text{ divides }\unicode[STIX]{x1D70E}(x)-x\text{ for all }x\in {\mathcal{O}}_{L}\},\nonumber\\ \displaystyle J_{H}({\mathcal{O}}_{L}) & := & \displaystyle \text{ideal of }{\mathcal{O}}_{L}\text{generated by }\unicode[STIX]{x1D70E}(x)-x\text{ for all }x\in {\mathcal{O}}_{L}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N({\mathcal{O}}_{L}) & := & \displaystyle \max \{k\mid \unicode[STIX]{x1D70B}^{k}\text{ divides }\unicode[STIX]{x1D70E}(x)-x\text{ for all }x\in {\mathcal{O}}_{L}\},\nonumber\\ \displaystyle J_{H}({\mathcal{O}}_{L}) & := & \displaystyle \text{ideal of }{\mathcal{O}}_{L}\text{generated by }\unicode[STIX]{x1D70E}(x)-x\text{ for all }x\in {\mathcal{O}}_{L}.\nonumber\end{eqnarray}$$
Since
![]() ${\mathcal{O}}_{L}$
is a DVR, the ideal
${\mathcal{O}}_{L}$
is a DVR, the ideal
 $J_{H}({\mathcal{O}}_{L})$
is principal. More precisely, this ideal is generated by
$J_{H}({\mathcal{O}}_{L})$
is principal. More precisely, this ideal is generated by
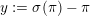 $y:=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D70B}$
, and it is also generated by
$y:=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70B})-\unicode[STIX]{x1D70B}$
, and it is also generated by
![]() $\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}$
. In [Reference Király and LütkebohmertKL13], ideals generated by elements of the form
$\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}$
. In [Reference Király and LütkebohmertKL13], ideals generated by elements of the form
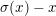 $\unicode[STIX]{x1D70E}(x)-x$
are called augmentation ideals. Also, it is not difficult to see that they do not depend on the choice of generator
$\unicode[STIX]{x1D70E}(x)-x$
are called augmentation ideals. Also, it is not difficult to see that they do not depend on the choice of generator
![]() $\unicode[STIX]{x1D70E}$
, which justifies the subscript
$\unicode[STIX]{x1D70E}$
, which justifies the subscript
![]() $H$
rather than
$H$
rather than
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Next, let
![]() $\widehat{{\mathcal{X}}}_{0}$
be the formal completion of
$\widehat{{\mathcal{X}}}_{0}$
be the formal completion of
![]() ${\mathcal{X}}$
along the special fiber
${\mathcal{X}}$
along the special fiber
![]() ${\mathcal{X}}_{0}$
, which is a formal scheme. For every point
${\mathcal{X}}_{0}$
, which is a formal scheme. For every point
![]() $x\in {\mathcal{X}}_{0}$
, we define
$x\in {\mathcal{X}}_{0}$
, we define
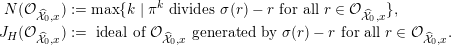 $$\begin{eqnarray}\displaystyle N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}) & := & \displaystyle \max \{k\mid \unicode[STIX]{x1D70B}^{k}\text{ divides }\unicode[STIX]{x1D70E}(r)-r\text{ for all }r\in {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}\},\nonumber\\ \displaystyle J_{H}({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}) & := & \displaystyle \text{ideal of }{\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}\text{generated by }\unicode[STIX]{x1D70E}(r)-r\text{ for all }r\in {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}) & := & \displaystyle \max \{k\mid \unicode[STIX]{x1D70B}^{k}\text{ divides }\unicode[STIX]{x1D70E}(r)-r\text{ for all }r\in {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}\},\nonumber\\ \displaystyle J_{H}({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}) & := & \displaystyle \text{ideal of }{\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}\text{generated by }\unicode[STIX]{x1D70E}(r)-r\text{ for all }r\in {\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}.\nonumber\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D702}\in {\mathcal{X}}_{0}$
denotes the generic point, then we have the following:
$\unicode[STIX]{x1D702}\in {\mathcal{X}}_{0}$
denotes the generic point, then we have the following:
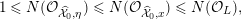 $$\begin{eqnarray}1\leqslant N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})\leqslant N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x})\leqslant N({\mathcal{O}}_{L}),\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})\leqslant N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x})\leqslant N({\mathcal{O}}_{L}),\end{eqnarray}$$
where the leftmost inequality follows from the triviality of the
![]() $H$
-action on
$H$
-action on
![]() ${\mathcal{X}}_{0}$
. We distinguish two cases.
${\mathcal{X}}_{0}$
. We distinguish two cases.
Case (I):
 $N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})<N({\mathcal{O}}_{L})$
.
$N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})<N({\mathcal{O}}_{L})$
.
Let
![]() $x\in {\mathcal{X}}_{0}$
be an arbitrary point and set
$x\in {\mathcal{X}}_{0}$
be an arbitrary point and set
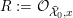 $R:={\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
and
$R:={\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
and
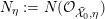 $N_{\unicode[STIX]{x1D702}}:=N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})$
. Then we define a map
$N_{\unicode[STIX]{x1D702}}:=N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})$
. Then we define a map
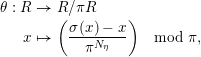 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:R & \rightarrow & \displaystyle R/\unicode[STIX]{x1D70B}R\nonumber\\ \displaystyle x & \mapsto & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70E}(x)-x}{\unicode[STIX]{x1D70B}^{N_{\unicode[STIX]{x1D702}}}}\biggr)\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D70B},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}:R & \rightarrow & \displaystyle R/\unicode[STIX]{x1D70B}R\nonumber\\ \displaystyle x & \mapsto & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70E}(x)-x}{\unicode[STIX]{x1D70B}^{N_{\unicode[STIX]{x1D702}}}}\biggr)\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D70B},\nonumber\end{eqnarray}$$
which is easily seen to be a derivation. Since we have
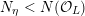 $N_{\unicode[STIX]{x1D702}}<N({\mathcal{O}}_{L})$
, we compute
$N_{\unicode[STIX]{x1D702}}<N({\mathcal{O}}_{L})$
, we compute
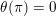 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B})=0$
, and thus
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70B})=0$
, and thus
![]() $\unicode[STIX]{x1D703}$
induces a derivation
$\unicode[STIX]{x1D703}$
induces a derivation
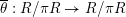 $\overline{\unicode[STIX]{x1D703}}:R/\unicode[STIX]{x1D70B}R\rightarrow R/\unicode[STIX]{x1D70B}R$
. This globalizes and gives rise to a derivation on the special fiber
$\overline{\unicode[STIX]{x1D703}}:R/\unicode[STIX]{x1D70B}R\rightarrow R/\unicode[STIX]{x1D70B}R$
. This globalizes and gives rise to a derivation on the special fiber
![]() ${\mathcal{X}}_{0}$
. It follows from the definition of
${\mathcal{X}}_{0}$
. It follows from the definition of
![]() $N_{\unicode[STIX]{x1D702}}$
that this derivation is non-zero at the generic point
$N_{\unicode[STIX]{x1D702}}$
that this derivation is non-zero at the generic point
![]() $\unicode[STIX]{x1D702}\in {\mathcal{X}}_{0}$
, whence non-trivial.
$\unicode[STIX]{x1D702}\in {\mathcal{X}}_{0}$
, whence non-trivial.
Case (II):
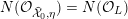 $N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})=N({\mathcal{O}}_{L})$
.
$N({\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},\unicode[STIX]{x1D702}})=N({\mathcal{O}}_{L})$
.
Let
![]() $x\in {\mathcal{X}}_{0}$
be an arbitrary point and set
$x\in {\mathcal{X}}_{0}$
be an arbitrary point and set
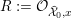 $R:={\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
. Then the two inequalities at the center and the right of (5) are equalities, which implies that all inclusions in
$R:={\mathcal{O}}_{\widehat{{\mathcal{X}}}_{0},x}$
. Then the two inequalities at the center and the right of (5) are equalities, which implies that all inclusions in
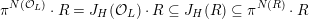 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}\cdot R=J_{H}({\mathcal{O}}_{L})\cdot R\subseteq J_{H}(R)\subseteq \unicode[STIX]{x1D70B}^{N(R)}\cdot R\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}\cdot R=J_{H}({\mathcal{O}}_{L})\cdot R\subseteq J_{H}(R)\subseteq \unicode[STIX]{x1D70B}^{N(R)}\cdot R\end{eqnarray}$$
are equalities. In particular,
![]() $J_{H}(R)$
is a principal ideal, generated by
$J_{H}(R)$
is a principal ideal, generated by
![]() $\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}$
. But then [Reference Király and LütkebohmertKL13, Proposition 5] implies that there is an isomorphism of
$\unicode[STIX]{x1D70B}^{N({\mathcal{O}}_{L})}$
. But then [Reference Király and LütkebohmertKL13, Proposition 5] implies that there is an isomorphism of
![]() $R^{H}$
- (respectively
$R^{H}$
- (respectively
![]() ${\mathcal{O}}_{L}^{H}$
-) modules
${\mathcal{O}}_{L}^{H}$
-) modules
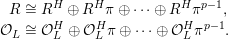 $$\begin{eqnarray}\displaystyle R & \cong & \displaystyle R^{H}\oplus R^{H}\unicode[STIX]{x1D70B}\oplus \cdots \oplus R^{H}\unicode[STIX]{x1D70B}^{p-1},\nonumber\\ \displaystyle {\mathcal{O}}_{L} & \cong & \displaystyle {\mathcal{O}}_{L}^{H}\oplus {\mathcal{O}}_{L}^{H}\unicode[STIX]{x1D70B}\oplus \cdots \oplus {\mathcal{O}}_{L}^{H}\unicode[STIX]{x1D70B}^{p-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R & \cong & \displaystyle R^{H}\oplus R^{H}\unicode[STIX]{x1D70B}\oplus \cdots \oplus R^{H}\unicode[STIX]{x1D70B}^{p-1},\nonumber\\ \displaystyle {\mathcal{O}}_{L} & \cong & \displaystyle {\mathcal{O}}_{L}^{H}\oplus {\mathcal{O}}_{L}^{H}\unicode[STIX]{x1D70B}\oplus \cdots \oplus {\mathcal{O}}_{L}^{H}\unicode[STIX]{x1D70B}^{p-1}.\nonumber\end{eqnarray}$$
From this description, we conclude that the natural map
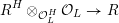 $$\begin{eqnarray}R^{H}\otimes _{{\mathcal{O}}_{L}^{H}}{\mathcal{O}}_{L}\rightarrow R\end{eqnarray}$$
$$\begin{eqnarray}R^{H}\otimes _{{\mathcal{O}}_{L}^{H}}{\mathcal{O}}_{L}\rightarrow R\end{eqnarray}$$
is an isomorphism. Moreover, if
![]() $\unicode[STIX]{x1D70B}^{H}$
is a uniformizer of
$\unicode[STIX]{x1D70B}^{H}$
is a uniformizer of
![]() ${\mathcal{O}}_{L}^{H}$
, then the previous isomorphism induces an isomorphism
${\mathcal{O}}_{L}^{H}$
, then the previous isomorphism induces an isomorphism
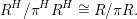 $$\begin{eqnarray}R^{H}/\unicode[STIX]{x1D70B}^{H}R^{H}\cong R/\unicode[STIX]{x1D70B}R.\end{eqnarray}$$
$$\begin{eqnarray}R^{H}/\unicode[STIX]{x1D70B}^{H}R^{H}\cong R/\unicode[STIX]{x1D70B}R.\end{eqnarray}$$
This local computation at completions shows that
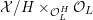 ${\mathcal{X}}/H\times _{{\mathcal{O}}_{L}^{H}}{\mathcal{O}}_{L}$
is isomorphic to
${\mathcal{X}}/H\times _{{\mathcal{O}}_{L}^{H}}{\mathcal{O}}_{L}$
is isomorphic to
![]() ${\mathcal{X}}$
, and that the special fiber
${\mathcal{X}}$
, and that the special fiber
![]() ${\mathcal{X}}_{0}$
of
${\mathcal{X}}_{0}$
of
![]() ${\mathcal{X}}$
is isomorphic to the special fiber of
${\mathcal{X}}$
is isomorphic to the special fiber of
![]() ${\mathcal{X}}/H$
. Since
${\mathcal{X}}/H$
. Since
![]() ${\mathcal{X}}$
is smooth over
${\mathcal{X}}$
is smooth over
![]() ${\mathcal{O}}_{L}$
,
${\mathcal{O}}_{L}$
,
![]() ${\mathcal{X}}_{0}$
is smooth over the residue field of
${\mathcal{X}}_{0}$
is smooth over the residue field of
![]() ${\mathcal{O}}_{L}$
, which implies that also the special fiber of
${\mathcal{O}}_{L}$
, which implies that also the special fiber of
![]() ${\mathcal{X}}/H$
is smooth over the residue field of
${\mathcal{X}}/H$
is smooth over the residue field of
![]() ${\mathcal{O}}_{L}^{H}$
. But this implies that
${\mathcal{O}}_{L}^{H}$
. But this implies that
![]() ${\mathcal{X}}/H$
is smooth over
${\mathcal{X}}/H$
is smooth over
![]() ${\mathcal{O}}_{L}^{H}$
.◻
${\mathcal{O}}_{L}^{H}$
.◻
Combining Propositions 5.9 and 5.11, we obtain the following result.
Corollary 5.12. Let
![]() $X$
be a smooth and proper variety over
$X$
be a smooth and proper variety over
![]() $K$
. Let
$K$
. Let
![]() $L/K$
be a finite Galois extension with group
$L/K$
be a finite Galois extension with group
![]() $G$
, such that
$G$
, such that
![]() $X_{L}$
admits a smooth model
$X_{L}$
admits a smooth model
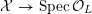 ${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Assume that the natural
${\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}$
. Assume that the natural
![]() $G$
-action on
$G$
-action on
![]() $X_{L}$
extends to
$X_{L}$
extends to
![]() ${\mathcal{X}}$
, and that the inertia subgroup
${\mathcal{X}}$
, and that the inertia subgroup
![]() $I_{G}$
of
$I_{G}$
of
![]() $G$
acts trivially on the special fiber
$G$
acts trivially on the special fiber
![]() ${\mathcal{X}}_{0}$
. Assume also that the special fiber
${\mathcal{X}}_{0}$
. Assume also that the special fiber
![]() ${\mathcal{X}}_{0}$
admits no non-trivial global vector fields. Then:
${\mathcal{X}}_{0}$
admits no non-trivial global vector fields. Then:
-
(i) the quotient
 ${\mathcal{X}}/I_{G}$
is smooth over
${\mathcal{X}}/I_{G}$
is smooth over
 ${\mathcal{O}}_{L}^{I_{G}}$
;
${\mathcal{O}}_{L}^{I_{G}}$
; -
(ii) the special fiber of
 ${\mathcal{X}}/I_{G}$
is isomorphic to
${\mathcal{X}}/I_{G}$
is isomorphic to
 ${\mathcal{X}}_{0}$
.
${\mathcal{X}}_{0}$
.
Proof. We have a short exact sequence
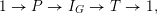 $$\begin{eqnarray}1\rightarrow P\rightarrow I_{G}\rightarrow T\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow P\rightarrow I_{G}\rightarrow T\rightarrow 1,\end{eqnarray}$$
where
![]() $P$
is the unique
$P$
is the unique
![]() $p$
-Sylow subgroup of
$p$
-Sylow subgroup of
![]() $I_{G}$
, and where
$I_{G}$
, and where
![]() $T$
is cyclic of order prime to
$T$
is cyclic of order prime to
![]() $p$
. By definition,
$p$
. By definition,
![]() $P$
is the wild inertia, and
$P$
is the wild inertia, and
![]() $T$
is the tame inertia.
$T$
is the tame inertia.
Being a
![]() $p$
-group,
$p$
-group,
![]() $P$
can be written as a successive extension of cyclic groups of order
$P$
can be written as a successive extension of cyclic groups of order
![]() $p$
. Thus, applying Proposition 5.11 inductively, we obtain a smooth algebraic space
$p$
. Thus, applying Proposition 5.11 inductively, we obtain a smooth algebraic space
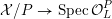 $$\begin{eqnarray}{\mathcal{X}}/P\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}^{P}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}/P\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}^{P}\end{eqnarray}$$
with special fiber
![]() ${\mathcal{X}}_{0}$
, which is a model of
${\mathcal{X}}_{0}$
, which is a model of
![]() $X_{L^{P}}$
.
$X_{L^{P}}$
.
Finally, applying Proposition 5.9 to the residual
![]() $T$
-action on
$T$
-action on
![]() ${\mathcal{X}}/P$
, we obtain a smooth algebraic space
${\mathcal{X}}/P$
, we obtain a smooth algebraic space
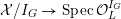 $$\begin{eqnarray}{\mathcal{X}}/I_{G}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}^{I_{G}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}/I_{G}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L}^{I_{G}}\end{eqnarray}$$
with special fiber
![]() ${\mathcal{X}}_{0}$
, which is a model of
${\mathcal{X}}_{0}$
, which is a model of
![]() $X_{L^{I_{G}}}$
.◻
$X_{L^{I_{G}}}$
.◻
Remark 5.13. If
![]() $X$
is a K3 surface, then the special fiber
$X$
is a K3 surface, then the special fiber
![]() ${\mathcal{X}}_{0}$
is also a K3 surface and thus admits no non-zero vector fields by a theorem of Rudakov and Shafarevich [Reference Rudakov and ShafarevichRS76].
${\mathcal{X}}_{0}$
is also a K3 surface and thus admits no non-zero vector fields by a theorem of Rudakov and Shafarevich [Reference Rudakov and ShafarevichRS76].
6 The Néron–Ogg–Shafarevich criterion
We now come to the main result of this article, which is a criterion for good reduction of K3 surfaces, similar to the classical Néron–Ogg–Shafarevich criterion for elliptic curves and its generalization to Abelian varieties by Serre and Tate. Then we give a couple of corollaries concerning potential good reduction, and good reduction after a tame extension. Finally, we relate the reduction behavior of a polarized K3 surface to that of its associated Kuga–Satake Abelian variety.
6.1 The criterion
Let us remind the reader of § 3.1, where we introduced Assumption
![]() $(\star )$
and established it in several cases.
$(\star )$
and established it in several cases.
Theorem 6.1. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
. If the
$(\star )$
. If the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
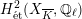 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for some
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for some
![]() $\ell \neq p$
, then we have the following.
$\ell \neq p$
, then we have the following.
-
(i) There exists a model of
 $X$
that is a projective scheme over
$X$
that is a projective scheme over
 ${\mathcal{O}}_{K}$
, whose special fiber is a K3 surface with at worst RDP singularities.
${\mathcal{O}}_{K}$
, whose special fiber is a K3 surface with at worst RDP singularities. -
(ii) There exists an integer
 $N$
, independent of
$N$
, independent of
 $X$
and
$X$
and
 $K$
, and a finite unramified extension
$K$
, and a finite unramified extension
 $L/K$
of degree at most
$L/K$
of degree at most
 $N$
such that
$N$
such that
 $X_{L}$
has good reduction over
$X_{L}$
has good reduction over
 $L$
.
$L$
.
Proof. By Theorem 3.3, there exists a finite Galois extension
![]() $M/K$
, say, with group
$M/K$
, say, with group
![]() $G$
and possibly ramified, such that there exists a smooth model of
$G$
and possibly ramified, such that there exists a smooth model of
![]() $X_{M}$
$X_{M}$
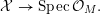 $$\begin{eqnarray}{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{M}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}\rightarrow \operatorname{Spec}{\mathcal{O}}_{M}.\end{eqnarray}$$
Choose an ample invertible sheaf
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $X$
. Then, by Proposition 4.5, we can replace
$X$
. Then, by Proposition 4.5, we can replace
![]() ${\mathcal{X}}$
by another smooth model of
${\mathcal{X}}$
by another smooth model of
![]() $X$
such that the pull-back of
$X$
such that the pull-back of
![]() ${\mathcal{L}}$
to
${\mathcal{L}}$
to
![]() $X_{M}$
restricts to an invertible sheaf on
$X_{M}$
restricts to an invertible sheaf on
![]() ${\mathcal{X}}_{0}$
that is big and nef.
${\mathcal{X}}_{0}$
that is big and nef.
Let
![]() $I_{G}$
be the inertia subgroup of
$I_{G}$
be the inertia subgroup of
![]() $G$
. By Proposition 5.5, the
$G$
. By Proposition 5.5, the
![]() $I_{G}$
-action extends to
$I_{G}$
-action extends to
![]() ${\mathcal{X}}$
and by Proposition 5.8, the induced
${\mathcal{X}}$
and by Proposition 5.8, the induced
![]() $I_{G}$
-action on the special fiber
$I_{G}$
-action on the special fiber
![]() ${\mathcal{X}}_{0}$
is trivial. Thus, by Corollary 5.12 and Remark 5.13, the quotient
${\mathcal{X}}_{0}$
is trivial. Thus, by Corollary 5.12 and Remark 5.13, the quotient
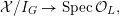 $$\begin{eqnarray}{\mathcal{X}}/I_{G}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}/I_{G}\rightarrow \operatorname{Spec}{\mathcal{O}}_{L},\end{eqnarray}$$
where
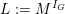 $L:=M^{I_{G}}$
, is a model of
$L:=M^{I_{G}}$
, is a model of
![]() $X_{L}$
. Since
$X_{L}$
. Since
![]() $L$
is a finite and unramified extension of
$L$
is a finite and unramified extension of
![]() $K$
, this establishes claim (ii) except for the universal bound
$K$
, this establishes claim (ii) except for the universal bound
![]() $N$
.
$N$
.
The pull-back of
![]() ${\mathcal{L}}$
to
${\mathcal{L}}$
to
![]() ${\mathcal{X}}/I_{G}$
is still ample on the generic fiber and big and nef when restricted to the special fiber. By Proposition 5.1, there exists a birational morphism over
${\mathcal{X}}/I_{G}$
is still ample on the generic fiber and big and nef when restricted to the special fiber. By Proposition 5.1, there exists a birational morphism over
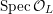 $\operatorname{Spec}{\mathcal{O}}_{L}$
$\operatorname{Spec}{\mathcal{O}}_{L}$
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\prime }:{\mathcal{X}}/I_{G}\rightarrow {\mathcal{Y}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{\prime }:{\mathcal{X}}/I_{G}\rightarrow {\mathcal{Y}},\end{eqnarray}$$
that is an isomorphism on generic fibers, such that the geometric special fiber
![]() ${\mathcal{Y}}_{0}$
is a K3 surface with at worst RDP singularities, and such that the
${\mathcal{Y}}_{0}$
is a K3 surface with at worst RDP singularities, and such that the
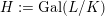 $H:=\operatorname{Gal}(L/K)$
-action on
$H:=\operatorname{Gal}(L/K)$
-action on
![]() $X_{L}$
extends to
$X_{L}$
extends to
![]() ${\mathcal{Y}}$
. Since
${\mathcal{Y}}$
. Since
![]() $L/K$
is unramified, the morphism
$L/K$
is unramified, the morphism
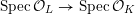 $\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
is étale, from which it follows that the quotient
$\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \operatorname{Spec}{\mathcal{O}}_{K}$
is étale, from which it follows that the quotient
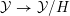 ${\mathcal{Y}}\rightarrow {\mathcal{Y}}/H$
is étale. Thus
${\mathcal{Y}}\rightarrow {\mathcal{Y}}/H$
is étale. Thus
![]() ${\mathcal{Y}}/H$
is a projective scheme over
${\mathcal{Y}}/H$
is a projective scheme over
![]() ${\mathcal{O}}_{K}$
, whose generic fiber is
${\mathcal{O}}_{K}$
, whose generic fiber is
![]() $X$
and whose geometric special fiber is a K3 surface with at worst RDP singularities. This establishes claim (i).
$X$
and whose geometric special fiber is a K3 surface with at worst RDP singularities. This establishes claim (i).
It remains to prove the existence of a universal bound
![]() $N$
in claim (ii). Since the Picard rank of a K3 surface is bounded above by
$N$
in claim (ii). Since the Picard rank of a K3 surface is bounded above by
![]() $22$
, there is only a finite list
$22$
, there is only a finite list
![]() $\mathsf{L}$
of Dynkin diagrams that is independent of the characteristic and whose associated root lattices can be embedded in the Néron–Severi lattice of a K3 surface. Therefore, a K3 surface over an algebraically closed field has at most
$\mathsf{L}$
of Dynkin diagrams that is independent of the characteristic and whose associated root lattices can be embedded in the Néron–Severi lattice of a K3 surface. Therefore, a K3 surface over an algebraically closed field has at most
![]() $21$
RDP singularities, and all of them are from the list
$21$
RDP singularities, and all of them are from the list
![]() $\mathsf{L}$
. By [Reference ArtinArt77], there exist only finitely many analytic isomorphism types of RDP singularities with fixed dual resolution graph over algebraically closed fields. For every
$\mathsf{L}$
. By [Reference ArtinArt77], there exist only finitely many analytic isomorphism types of RDP singularities with fixed dual resolution graph over algebraically closed fields. For every
![]() $k^{\prime }$
-rational singularity over some perfect field
$k^{\prime }$
-rational singularity over some perfect field
![]() $k^{\prime }$
that becomes analytically isomorphic to a RDP singularity over
$k^{\prime }$
that becomes analytically isomorphic to a RDP singularity over
![]() $\overline{k}^{\prime }$
, we have a versal deformation space
$\overline{k}^{\prime }$
, we have a versal deformation space
![]() $\operatorname{Def}$
over
$\operatorname{Def}$
over
![]() $k^{\prime }$
or
$k^{\prime }$
or
![]() $W(k^{\prime })$
(if
$W(k^{\prime })$
(if
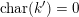 $\operatorname{char}(k^{\prime })=0$
or
$\operatorname{char}(k^{\prime })=0$
or
![]() ${>}0$
, respectively) and a simultaneous resolution algebraic space
${>}0$
, respectively) and a simultaneous resolution algebraic space
![]() $\operatorname{Res}$
, which is finite over
$\operatorname{Res}$
, which is finite over
![]() $\operatorname{Def}$
by [Reference ArtinArt74, Theorem 3]. Since deformation and resolution spaces solve universal problems, the degree of
$\operatorname{Def}$
by [Reference ArtinArt74, Theorem 3]. Since deformation and resolution spaces solve universal problems, the degree of
 $\operatorname{Res}\rightarrow \operatorname{Def}$
depends only on the analytic isomorphism type of the singularity over
$\operatorname{Res}\rightarrow \operatorname{Def}$
depends only on the analytic isomorphism type of the singularity over
![]() $\overline{k}^{\prime }$
. In particular, there exists an integer
$\overline{k}^{\prime }$
. In particular, there exists an integer
![]() $N^{\prime }$
such that every deformation of a
$N^{\prime }$
such that every deformation of a
![]() $k^{\prime }$
-rational singularity over
$k^{\prime }$
-rational singularity over
![]() $k^{\prime }$
that becomes a RDP singularity over
$k^{\prime }$
that becomes a RDP singularity over
![]() $\overline{k}^{\prime }$
from the list
$\overline{k}^{\prime }$
from the list
![]() $\mathsf{L}$
can be resolved after an extension of degree at most
$\mathsf{L}$
can be resolved after an extension of degree at most
![]() $N^{\prime }$
. For each Dynkin diagram in
$N^{\prime }$
. For each Dynkin diagram in
![]() $\mathsf{L}$
and for almost every characteristic (in fact, it suffices to exclude
$\mathsf{L}$
and for almost every characteristic (in fact, it suffices to exclude
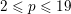 $2\leqslant p\leqslant 19$
), there is only one analytic isomorphism type of RDP singularities and the corresponding degree of
$2\leqslant p\leqslant 19$
), there is only one analytic isomorphism type of RDP singularities and the corresponding degree of
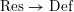 $\operatorname{Res}\rightarrow \operatorname{Def}$
is independent of the characteristic. Therefore, the bound
$\operatorname{Res}\rightarrow \operatorname{Def}$
is independent of the characteristic. Therefore, the bound
![]() $N^{\prime }$
can be taken to be independent of the characteristic.
$N^{\prime }$
can be taken to be independent of the characteristic.
Now, let
![]() ${\mathcal{Y}}_{0}$
be the special fiber of
${\mathcal{Y}}_{0}$
be the special fiber of
![]() ${\mathcal{Y}}$
. Since
${\mathcal{Y}}$
. Since
![]() $({\mathcal{Y}}_{0})_{\overline{k}}$
has at most
$({\mathcal{Y}}_{0})_{\overline{k}}$
has at most
![]() $21$
non-smooth points, all non-smooth points of
$21$
non-smooth points, all non-smooth points of
![]() ${\mathcal{Y}}_{0}$
become
${\mathcal{Y}}_{0}$
become
![]() $k^{\prime }$
-rational after some finite extension
$k^{\prime }$
-rational after some finite extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
of degree
$k$
of degree
![]() ${\leqslant}21!$
. Let
${\leqslant}21!$
. Let
![]() $K^{\prime }/K$
be the corresponding unramified extension of
$K^{\prime }/K$
be the corresponding unramified extension of
![]() $K$
. From the previous discussion, it follows that after a (possibly ramified) extension
$K$
. From the previous discussion, it follows that after a (possibly ramified) extension
![]() $L/K^{\prime }$
of degree at most
$L/K^{\prime }$
of degree at most
![]() ${N^{\prime }}^{21}$
, the surface
${N^{\prime }}^{21}$
, the surface
![]() $X_{L}$
has good reduction. By the above arguments, we can descend a smooth model of
$X_{L}$
has good reduction. By the above arguments, we can descend a smooth model of
![]() $X_{L}$
over
$X_{L}$
over
![]() ${\mathcal{O}}_{L}$
to the maximal unramified subextension
${\mathcal{O}}_{L}$
to the maximal unramified subextension
![]() $M$
of
$M$
of
![]() $L/K^{\prime }$
. Thus
$L/K^{\prime }$
. Thus
![]() $X_{M}$
has good reduction, and
$X_{M}$
has good reduction, and
![]() $M/K$
is an unramified extension of degree at most
$M/K$
is an unramified extension of degree at most
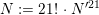 $N:=21!\,\cdot {N^{\prime }}^{21}$
. This establishes the bound claimed in (ii).◻
$N:=21!\,\cdot {N^{\prime }}^{21}$
. This establishes the bound claimed in (ii).◻
Remark 6.2. In the statement (ii) of Theorem 6.1, we cannot avoid field extensions in general: in the next section, we will give examples of K3 surfaces
![]() $X$
over
$X$
over
![]() $\mathbb{Q}_{p}$
with unramified
$\mathbb{Q}_{p}$
with unramified
![]() $G_{\mathbb{Q}_{p}}$
-representations on
$G_{\mathbb{Q}_{p}}$
-representations on
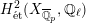 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
that do not admit smooth models over
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
that do not admit smooth models over
![]() $\mathbb{Z}_{p}$
.
$\mathbb{Z}_{p}$
.
Remark 6.3. Unlike curves and Abelian varieties, even if a K3 surface has good reduction over
![]() $L$
, then a smooth model of
$L$
, then a smooth model of
![]() $X_{L}$
over
$X_{L}$
over
![]() ${\mathcal{O}}_{L}$
need not be unique. However, by Proposition 4.7, the special fibers of all smooth models are isomorphic and the models are connected by finite sequences of flopping contractions and their inverses (similar to the classical Atiyah flop).
${\mathcal{O}}_{L}$
need not be unique. However, by Proposition 4.7, the special fibers of all smooth models are isomorphic and the models are connected by finite sequences of flopping contractions and their inverses (similar to the classical Atiyah flop).
If a smooth variety over
![]() $K$
has good reduction over an unramified extension, then the
$K$
has good reduction over an unramified extension, then the
![]() $G_{K}$
-representations on
$G_{K}$
-representations on
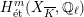 $H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
are unramified for all
$H_{\acute{\text{e}}\text{t}}^{m}(X_{\overline{K}},\mathbb{Q}_{\ell })$
are unramified for all
![]() $m$
and for all
$m$
and for all
![]() $\ell \neq p$
by Theorem 2.4. Thus, as in the case of Abelian varieties in [Reference Serre and TateST68, Corollary 1 of Theorem 1], we obtain the following independence of the auxiliary prime
$\ell \neq p$
by Theorem 2.4. Thus, as in the case of Abelian varieties in [Reference Serre and TateST68, Corollary 1 of Theorem 1], we obtain the following independence of the auxiliary prime
![]() $\ell$
.
$\ell$
.
Corollary 6.4. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
that satisfies Assumption
$K$
that satisfies Assumption
![]() $(\star )$
. Then the
$(\star )$
. Then the
![]() $G_{K}$
-representation on
$G_{K}$
-representation on
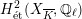 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })$
is unramified for one
![]() $\ell \neq p$
if and only if it is unramified for all
$\ell \neq p$
if and only if it is unramified for all
![]() $\ell \neq p$
.
$\ell \neq p$
.
We remark that this independence of
![]() $\ell$
can be also derived from the weaker criterion of [Reference MatsumotoMat15] (Theorem 3.3), combined with Ochiai’s independence of traces [Reference OchiaiOch99, Theorem B].
$\ell$
can be also derived from the weaker criterion of [Reference MatsumotoMat15] (Theorem 3.3), combined with Ochiai’s independence of traces [Reference OchiaiOch99, Theorem B].
We leave the following easy consequence of Theorem 6.1 to the reader (this also can be derived from the criterion of [Reference MatsumotoMat15]).
Corollary 6.5. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
such that the image of inertia
$K$
such that the image of inertia
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:I_{K}\rightarrow \operatorname{GL}(H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:I_{K}\rightarrow \operatorname{GL}(H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell }))\end{eqnarray}$$
is finite. If
![]() $X$
satisfies Assumption
$X$
satisfies Assumption
![]() $(\star )$
, then
$(\star )$
, then
![]() $X$
has potential good reduction. ◻
$X$
has potential good reduction. ◻
If a
![]() $g$
-dimensional Abelian variety over
$g$
-dimensional Abelian variety over
![]() $K$
with
$K$
with
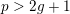 $p>2g+1$
has potential good reduction, then good reduction can be achieved over a tame extension of
$p>2g+1$
has potential good reduction, then good reduction can be achieved over a tame extension of
![]() $K$
by [Reference Serre and TateST68, Corollary 2 of Theorem 2]. We have the following analog for K3 surfaces.
$K$
by [Reference Serre and TateST68, Corollary 2 of Theorem 2]. We have the following analog for K3 surfaces.
Corollary 6.6. Let
![]() $X$
be a K3 surface over
$X$
be a K3 surface over
![]() $K$
with potential good reduction. If
$K$
with potential good reduction. If
![]() $p\geqslant 23$
, then good reduction can be achieved after a tame extension.
$p\geqslant 23$
, then good reduction can be achieved after a tame extension.
Proof. The idea of proof is the same as for Abelian varieties in [Reference Serre and TateST68], we only adjust the arguments to our situation: since
![]() $X$
is projective, there exists an ample invertible sheaf
$X$
is projective, there exists an ample invertible sheaf
![]() ${\mathcal{L}}$
defined over
${\mathcal{L}}$
defined over
![]() $K$
, and then its Chern class
$K$
, and then its Chern class
![]() $c_{1}({\mathcal{L}})$
gives rise to a
$c_{1}({\mathcal{L}})$
gives rise to a
![]() $G_{K}$
-invariant class in
$G_{K}$
-invariant class in
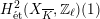 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
. Let
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
. Let
![]() $T_{\ell }^{2}$
be the orthogonal complement of
$T_{\ell }^{2}$
be the orthogonal complement of
![]() $c_{1}({\mathcal{L}})$
with respect to the Poincaré duality pairing. For
$c_{1}({\mathcal{L}})$
with respect to the Poincaré duality pairing. For
![]() $\ell \neq p$
, we let
$\ell \neq p$
, we let
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:G_{K}\rightarrow \operatorname{GL}(T_{\ell }^{2})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\ell }:G_{K}\rightarrow \operatorname{GL}(T_{\ell }^{2})\end{eqnarray}$$
be the induced
![]() $\ell$
-adic Galois representation, and denote by
$\ell$
-adic Galois representation, and denote by
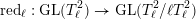 $$\begin{eqnarray}\operatorname{red}_{\ell }:\operatorname{GL}(T_{\ell }^{2})\rightarrow \operatorname{GL}(T_{\ell }^{2}/\ell T_{\ell }^{2})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{red}_{\ell }:\operatorname{GL}(T_{\ell }^{2})\rightarrow \operatorname{GL}(T_{\ell }^{2}/\ell T_{\ell }^{2})\end{eqnarray}$$
its reduction modulo
![]() $\ell$
. As usual, we denote by
$\ell$
. As usual, we denote by
![]() $I_{K}$
(respectively,
$I_{K}$
(respectively,
![]() $P_{K}$
) the inertia (respectively, wild inertia) subgroup of
$P_{K}$
) the inertia (respectively, wild inertia) subgroup of
![]() $G_{K}$
. Since
$G_{K}$
. Since
![]() $X$
has potential good reduction,
$X$
has potential good reduction,
![]() $\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is a finite group. Moreover, if
$\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is a finite group. Moreover, if
![]() $\ell$
is odd, since
$\ell$
is odd, since
![]() $\ker \operatorname{red}_{\ell }$
has no non-trivial element of finite order (as can be seen by taking the logarithm),
$\ker \operatorname{red}_{\ell }$
has no non-trivial element of finite order (as can be seen by taking the logarithm),
![]() $\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is isomorphic to
$\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is isomorphic to
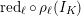 $\operatorname{red}_{\ell }\circ \,\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
via
$\operatorname{red}_{\ell }\circ \,\unicode[STIX]{x1D70C}_{\ell }(I_{K})$
via
![]() $\operatorname{red}_{\ell }$
.
$\operatorname{red}_{\ell }$
.
Now, suppose that
![]() $\unicode[STIX]{x1D70C}_{\ell }(P_{K})$
is non-trivial. Then the order of
$\unicode[STIX]{x1D70C}_{\ell }(P_{K})$
is non-trivial. Then the order of
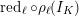 $\operatorname{red}_{\ell }\circ \unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is divisible by
$\operatorname{red}_{\ell }\circ \unicode[STIX]{x1D70C}_{\ell }(I_{K})$
is divisible by
![]() $p$
for all odd
$p$
for all odd
![]() $\ell$
. In particular, if we set
$\ell$
. In particular, if we set
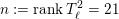 $n:=\operatorname{rank}T_{\ell }^{2}=21$
, then
$n:=\operatorname{rank}T_{\ell }^{2}=21$
, then
![]() $p$
divides the order
$p$
divides the order
 $$\begin{eqnarray}|\!\operatorname{GL}_{n}(\mathbb{F}_{\ell })|=\ell ^{n(n-1)/2}\mathop{\prod }_{s=1}^{n}(\ell ^{s}-1)\end{eqnarray}$$
$$\begin{eqnarray}|\!\operatorname{GL}_{n}(\mathbb{F}_{\ell })|=\ell ^{n(n-1)/2}\mathop{\prod }_{s=1}^{n}(\ell ^{s}-1)\end{eqnarray}$$
for all odd
![]() $\ell$
. By Dirichlet’s theorem on arithmetic progressions, there exist infinitely many primes
$\ell$
. By Dirichlet’s theorem on arithmetic progressions, there exist infinitely many primes
![]() $\ell$
such that the residue class of
$\ell$
such that the residue class of
![]() $\ell$
modulo
$\ell$
modulo
![]() $p$
generates the group
$p$
generates the group
![]() $\mathbb{F}_{p}^{\times }$
, which is of order
$\mathbb{F}_{p}^{\times }$
, which is of order
![]() $p-1$
. Choosing such an
$p-1$
. Choosing such an
![]() $\ell$
, we obtain the estimate
$\ell$
, we obtain the estimate
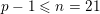 $p-1\leqslant n=21$
. (When working directly with
$p-1\leqslant n=21$
. (When working directly with
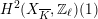 $H^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
instead of the primitive cohomology group
$H^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
instead of the primitive cohomology group
![]() $T_{\ell }^{2}$
, we only get the estimate
$T_{\ell }^{2}$
, we only get the estimate
 $p-1\leqslant 22$
, which includes the prime
$p-1\leqslant 22$
, which includes the prime
![]() $p=23$
.)
$p=23$
.)
Thus if
![]() $p\geqslant 23$
, then
$p\geqslant 23$
, then
![]() $\unicode[STIX]{x1D70C}_{\ell }(P_{K})$
is trivial. But then also the
$\unicode[STIX]{x1D70C}_{\ell }(P_{K})$
is trivial. But then also the
![]() $P_{K}$
-action on
$P_{K}$
-action on
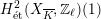 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
is trivial. Thus there exists a tame extension
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Z}_{\ell })(1)$
is trivial. Thus there exists a tame extension
![]() $L/K$
such that the
$L/K$
such that the
![]() $G_{L}$
-action on
$G_{L}$
-action on
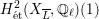 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })(1)$
is unramified. By Theorem 6.1, there exists an unramified extension of
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{L}},\mathbb{Q}_{\ell })(1)$
is unramified. By Theorem 6.1, there exists an unramified extension of
![]() $L^{\prime }/L$
such that
$L^{\prime }/L$
such that
![]() $X_{L^{\prime }}$
has good reduction. In particular,
$X_{L^{\prime }}$
has good reduction. In particular,
![]() $X$
has good reduction after a tame extension of
$X$
has good reduction after a tame extension of
![]() $K$
.◻
$K$
.◻
6.2 Kuga–Satake varieties
Given a polarized K3 surface
![]() $(X,{\mathcal{L}})$
over
$(X,{\mathcal{L}})$
over
![]() $\mathbb{C}$
, Kuga and Satake [Reference Kuga and SatakeKS67] associated to it a polarized Abelian variety, the Kuga–Satake Abelian variety
$\mathbb{C}$
, Kuga and Satake [Reference Kuga and SatakeKS67] associated to it a polarized Abelian variety, the Kuga–Satake Abelian variety
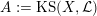 $A:=\operatorname{KS}(X,{\mathcal{L}})$
, which is of dimension
$A:=\operatorname{KS}(X,{\mathcal{L}})$
, which is of dimension
![]() $2^{19}$
. Although their construction is transcendental, it is shown in work of Rizov [Reference RizovRiz10] and Madapusi Pera [Reference Madapusi PeraMad15], building on previous results of Deligne [Reference DeligneDel72] and André [Reference AndréAnd96], that the Kuga–Satake construction exists over arbitrary fields: namely, if
$2^{19}$
. Although their construction is transcendental, it is shown in work of Rizov [Reference RizovRiz10] and Madapusi Pera [Reference Madapusi PeraMad15], building on previous results of Deligne [Reference DeligneDel72] and André [Reference AndréAnd96], that the Kuga–Satake construction exists over arbitrary fields: namely, if
![]() $(X,{\mathcal{L}})$
is a polarized K3 surface over some field
$(X,{\mathcal{L}})$
is a polarized K3 surface over some field
![]() $k$
, then
$k$
, then
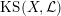 $\operatorname{KS}(X,{\mathcal{L}})$
exists over some finite extension of
$\operatorname{KS}(X,{\mathcal{L}})$
exists over some finite extension of
![]() $k$
. Then we have the following relation between good reduction of
$k$
. Then we have the following relation between good reduction of
![]() $(X,{\mathcal{L}})$
and
$(X,{\mathcal{L}})$
and
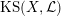 $\operatorname{KS}(X,{\mathcal{L}})$
.
$\operatorname{KS}(X,{\mathcal{L}})$
.
Theorem 6.7. Assume
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $(X,{\mathcal{L}})$
be a polarized K3 surface over
$(X,{\mathcal{L}})$
be a polarized K3 surface over
![]() $K$
.
$K$
.
-
(i) If
 $X$
has good reduction, then
$X$
has good reduction, then
 $\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
$\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
 $L/K$
, and it has good reduction over
$L/K$
, and it has good reduction over
 $L$
.
$L$
. -
(ii) Assume that
 $X$
satisfies Assumption
$X$
satisfies Assumption
 $(\star )$
. Let
$(\star )$
. Let
 $L/K$
be a field extension such that both
$L/K$
be a field extension such that both
 $\operatorname{KS}(X,{\mathcal{L}})$
and the Kuga–Satake correspondence (described below) can be defined over
$\operatorname{KS}(X,{\mathcal{L}})$
and the Kuga–Satake correspondence (described below) can be defined over
 $L$
. If
$L$
. If
 $\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
$\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
 $L$
, then
$L$
, then
 $X$
has good reduction over an unramified extension of
$X$
has good reduction over an unramified extension of
 $L$
.
$L$
.
Proof. We will use the notation and definitions of [Reference Madapusi PeraMad15].
(i) The pair
![]() $(X,{\mathcal{L}})$
gives rise to a morphism
$(X,{\mathcal{L}})$
gives rise to a morphism
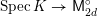 $\operatorname{Spec}K\rightarrow \mathsf{M}_{2d}^{\circ }$
, where
$\operatorname{Spec}K\rightarrow \mathsf{M}_{2d}^{\circ }$
, where
![]() $\mathsf{M}_{2d}^{\circ }$
denotes the moduli space of primitively polarized K3 surfaces of degree
$\mathsf{M}_{2d}^{\circ }$
denotes the moduli space of primitively polarized K3 surfaces of degree
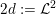 $2d:={\mathcal{L}}^{2}$
. By assumption, there exists a smooth model of
$2d:={\mathcal{L}}^{2}$
. By assumption, there exists a smooth model of
![]() $X$
over
$X$
over
![]() ${\mathcal{O}}_{K}$
, and by Proposition 4.5, there even exists a smooth model
${\mathcal{O}}_{K}$
, and by Proposition 4.5, there even exists a smooth model
![]() ${\mathcal{X}}$
of
${\mathcal{X}}$
of
![]() $X$
over
$X$
over
![]() ${\mathcal{O}}_{K}$
, such that the restriction of
${\mathcal{O}}_{K}$
, such that the restriction of
![]() ${\mathcal{L}}$
to the special fiber is big and nef. Thus the morphism
${\mathcal{L}}$
to the special fiber is big and nef. Thus the morphism
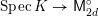 $\operatorname{Spec}K\rightarrow \mathsf{M}_{2d}^{\circ }$
extends to a morphism
$\operatorname{Spec}K\rightarrow \mathsf{M}_{2d}^{\circ }$
extends to a morphism
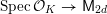 $\operatorname{Spec}{\mathcal{O}}_{K}\rightarrow \mathsf{M}_{2d}$
, where
$\operatorname{Spec}{\mathcal{O}}_{K}\rightarrow \mathsf{M}_{2d}$
, where
![]() $\mathsf{M}_{2d}$
denotes the moduli space of primitively quasi-polarized K3 surfaces of degree
$\mathsf{M}_{2d}$
denotes the moduli space of primitively quasi-polarized K3 surfaces of degree
![]() $2d$
. Passing to an unramified extension
$2d$
. Passing to an unramified extension
![]() $L/K$
of degree
$L/K$
of degree
![]() ${\leqslant}2$
if necessary, the previous classifying morphism extends to a morphism
${\leqslant}2$
if necessary, the previous classifying morphism extends to a morphism
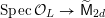 $\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \widetilde{\mathsf{M}}_{2d}$
, see [Reference Madapusi PeraMad15, §5]. Composing with the morphism
$\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \widetilde{\mathsf{M}}_{2d}$
, see [Reference Madapusi PeraMad15, §5]. Composing with the morphism
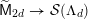 $\widetilde{\mathsf{M}}_{2d}\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
from [Reference Madapusi PeraMad15, Proposition 5.7], we obtain a morphism
$\widetilde{\mathsf{M}}_{2d}\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
from [Reference Madapusi PeraMad15, Proposition 5.7], we obtain a morphism
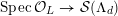 $\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
. We recall from [Reference Madapusi PeraMad15, §4] that there exists a finite and étale cover
$\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
. We recall from [Reference Madapusi PeraMad15, §4] that there exists a finite and étale cover
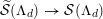 $\widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
, such that the Kuga–Satake Abelian scheme is a relative Abelian scheme over
$\widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})\rightarrow {\mathcal{S}}(\unicode[STIX]{x1D6EC}_{d})$
, such that the Kuga–Satake Abelian scheme is a relative Abelian scheme over
![]() $\widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})$
. Thus, after replacing
$\widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})$
. Thus, after replacing
![]() $L$
by a finite and unramified extension if necessary, we can lift the latter morphism to a morphism
$L$
by a finite and unramified extension if necessary, we can lift the latter morphism to a morphism
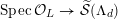 $\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})$
. Thus we obtain a Kuga–Satake Abelian variety
$\operatorname{Spec}{\mathcal{O}}_{L}\rightarrow \widetilde{{\mathcal{S}}}(\unicode[STIX]{x1D6EC}_{d})$
. Thus we obtain a Kuga–Satake Abelian variety
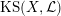 $\operatorname{KS}(X,{\mathcal{L}})$
over
$\operatorname{KS}(X,{\mathcal{L}})$
over
![]() $L$
that has good reduction, and where
$L$
that has good reduction, and where
![]() $L$
is an unramified extension of
$L$
is an unramified extension of
![]() $K$
.
$K$
.
(ii) By assumption,
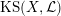 $\operatorname{KS}(X,{\mathcal{L}})$
is defined over
$\operatorname{KS}(X,{\mathcal{L}})$
is defined over
![]() $L$
and has good reduction over
$L$
and has good reduction over
![]() $L$
. Thus the
$L$
. Thus the
![]() $G_{L}$
-action on
$G_{L}$
-action on
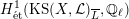 $H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{KS}(X,{\mathcal{L}})_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified. By the usual properties of the Kuga–Satake construction, there exists an embedding
$H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{KS}(X,{\mathcal{L}})_{\overline{L}},\mathbb{Q}_{\ell })$
is unramified. By the usual properties of the Kuga–Satake construction, there exists an embedding
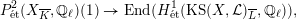 $$\begin{eqnarray}P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)\rightarrow \operatorname{End}(H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{KS}(X,{\mathcal{L}})_{\overline{L}},\mathbb{Q}_{\ell })),\end{eqnarray}$$
$$\begin{eqnarray}P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)\rightarrow \operatorname{End}(H_{\acute{\text{e}}\text{t}}^{1}(\operatorname{KS}(X,{\mathcal{L}})_{\overline{L}},\mathbb{Q}_{\ell })),\end{eqnarray}$$
where
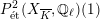 $P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
denotes the orthogonal complement of
$P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
denotes the orthogonal complement of
![]() $c_{1}({\mathcal{L}})$
inside
$c_{1}({\mathcal{L}})$
inside
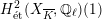 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
, and this embedding is
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
, and this embedding is
![]() $G_{L}$
-equivariant by assumption. This implies that also the
$G_{L}$
-equivariant by assumption. This implies that also the
![]() $G_{L}$
-action on
$G_{L}$
-action on
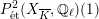 $P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is unramified. Since
$P_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is unramified. Since
![]() ${\mathcal{L}}$
is defined over
${\mathcal{L}}$
is defined over
![]() $K$
, the
$K$
, the
![]() $G_{L}$
-action on the
$G_{L}$
-action on the
![]() $\mathbb{Q}_{\ell }$
-subvector space generated by
$\mathbb{Q}_{\ell }$
-subvector space generated by
![]() $c_{1}({\mathcal{L}})$
inside
$c_{1}({\mathcal{L}})$
inside
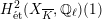 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is trivial. From this, we conclude that the
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is trivial. From this, we conclude that the
![]() $G_{L}$
-action on
$G_{L}$
-action on
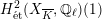 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is unramified. By Theorem 6.1,
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{K}},\mathbb{Q}_{\ell })(1)$
is unramified. By Theorem 6.1,
![]() $X$
has good reduction over an unramified extension of
$X$
has good reduction over an unramified extension of
![]() $L$
.◻
$L$
.◻
Remark 6.8. Let us make two comments.
(i) If
![]() $(X,{\mathcal{L}})$
is a polarized K3 surface with good reduction, then the previous theorem asserts that
$(X,{\mathcal{L}})$
is a polarized K3 surface with good reduction, then the previous theorem asserts that
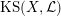 $\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
$\operatorname{KS}(X,{\mathcal{L}})$
can be defined over an unramified extension
![]() $L$
of
$L$
of
![]() $K$
. Thus if
$K$
. Thus if
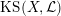 $\operatorname{KS}(X,{\mathcal{L}})$
can be descended to some field
$\operatorname{KS}(X,{\mathcal{L}})$
can be descended to some field
![]() $K^{\prime }$
with
$K^{\prime }$
with
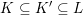 $K\subseteq K^{\prime }\subseteq L$
(so far, not much is known about fields of definition of Kuga–Satake Abelian varieties), then, since
$K\subseteq K^{\prime }\subseteq L$
(so far, not much is known about fields of definition of Kuga–Satake Abelian varieties), then, since
![]() $L/K^{\prime }$
is unramified and since
$L/K^{\prime }$
is unramified and since
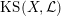 $\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
$\operatorname{KS}(X,{\mathcal{L}})$
has good reduction over
![]() $L$
by the previous theorem, the descended Abelian variety will have good reduction over
$L$
by the previous theorem, the descended Abelian variety will have good reduction over
![]() $K^{\prime }$
by [Reference Serre and TateST68].
$K^{\prime }$
by [Reference Serre and TateST68].
(ii) We can almost remove the
![]() $p\neq 2$
hypothesis in Theorem 6.7: by [Reference Kim and Madapusi PeraKM16, Proposition A.12] (see also the proof of [Reference Kim and Madapusi PeraKM16, Theorem A.1]), there exists a Kuga–Satake morphism with the properties needed to make the proof of Theorem 6.7 work also in residue characteristic 2, but so far only outside the locus of superspecial K3 surfaces.
$p\neq 2$
hypothesis in Theorem 6.7: by [Reference Kim and Madapusi PeraKM16, Proposition A.12] (see also the proof of [Reference Kim and Madapusi PeraKM16, Theorem A.1]), there exists a Kuga–Satake morphism with the properties needed to make the proof of Theorem 6.7 work also in residue characteristic 2, but so far only outside the locus of superspecial K3 surfaces.
7 Counterexamples
In this final section we give examples of K3 surfaces
![]() $X$
over
$X$
over
![]() $\mathbb{Q}_{p}$
for all
$\mathbb{Q}_{p}$
for all
![]() $p\geqslant 5$
with unramified
$p\geqslant 5$
with unramified
![]() $G_{\mathbb{Q}_{p}}$
-representation on
$G_{\mathbb{Q}_{p}}$
-representation on
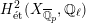 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
that do not have good reduction over
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
that do not have good reduction over
![]() $\mathbb{Q}_{p}$
. In particular, the unramified extension from Theorem 6.1 needed to obtain good reduction may be non-trivial. The examples in question already appeared in [Reference MatsumotoMat15, §5.3] and rest on examples due to van Luijk [Reference van LuijkvanL07, §3].
$\mathbb{Q}_{p}$
. In particular, the unramified extension from Theorem 6.1 needed to obtain good reduction may be non-trivial. The examples in question already appeared in [Reference MatsumotoMat15, §5.3] and rest on examples due to van Luijk [Reference van LuijkvanL07, §3].
Example 7.1. Fix a prime
![]() $p\geqslant 5$
. We choose integers
$p\geqslant 5$
. We choose integers
![]() $a,c$
such that
$a,c$
such that
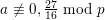 $a\not \equiv 0,\frac{27}{16}~\text{mod}~p$
, such that
$a\not \equiv 0,\frac{27}{16}~\text{mod}~p$
, such that
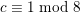 $c\equiv 1~\text{mod}~8$
, and such that
$c\equiv 1~\text{mod}~8$
, and such that
![]() $c$
is not a quadratic residue modulo
$c$
is not a quadratic residue modulo
![]() $p$
. Then we choose a homogeneous polynomial
$p$
. Then we choose a homogeneous polynomial
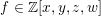 $f\in \mathbb{Z}[x,y,z,w]$
of degree
$f\in \mathbb{Z}[x,y,z,w]$
of degree
![]() $3$
, such that the following congruences hold:
$3$
, such that the following congruences hold:
 $$\begin{eqnarray}\displaystyle f & \equiv & \displaystyle \unicode[STIX]{x1D719}\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle f & \equiv & \displaystyle x^{3}+y^{3}+z^{3}+aw^{3}\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f & \equiv & \displaystyle \unicode[STIX]{x1D719}\hspace{0.6em}{\rm mod}\hspace{0.2em}2,\nonumber\\ \displaystyle f & \equiv & \displaystyle x^{3}+y^{3}+z^{3}+aw^{3}\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}$
is as in Example 5.4. Finally, we define the quartic hypersurface
$\unicode[STIX]{x1D719}$
is as in Example 5.4. Finally, we define the quartic hypersurface
 $$\begin{eqnarray}{\mathcal{X}}:={\mathcal{X}}(p):=\biggl\{wf+\biggl(pz^{2}+xy+\frac{p}{2}yz\biggr)^{2}-\frac{cp^{2}}{4}y^{2}z^{2}=0\biggr\}\subset \mathbb{P}_{\mathbb{ Z}_{p}}^{3},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{X}}:={\mathcal{X}}(p):=\biggl\{wf+\biggl(pz^{2}+xy+\frac{p}{2}yz\biggr)^{2}-\frac{cp^{2}}{4}y^{2}z^{2}=0\biggr\}\subset \mathbb{P}_{\mathbb{ Z}_{p}}^{3},\end{eqnarray}$$
and denote by
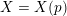 $X=X(p)$
its generic fiber.
$X=X(p)$
its generic fiber.
Theorem 7.2. Let
![]() $p\geqslant 5$
and let
$p\geqslant 5$
and let
![]() $X$
and
$X$
and
![]() ${\mathcal{X}}$
be as in Example 7.1. Then
${\mathcal{X}}$
be as in Example 7.1. Then
![]() $X$
is a smooth K3 surface over
$X$
is a smooth K3 surface over
![]() $\mathbb{Q}_{p}$
, such that:
$\mathbb{Q}_{p}$
, such that:
-
(i) the
 $G_{\mathbb{Q}_{p}}$
-representation on
$G_{\mathbb{Q}_{p}}$
-representation on
 $H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
$H_{\acute{\text{e}}\text{t}}^{2}(X_{\overline{\mathbb{Q}}_{p}},\mathbb{Q}_{\ell })$
is unramified for all
 $\ell \neq p$
;
$\ell \neq p$
; -
(ii)
 ${\mathcal{X}}$
is a projective model of
${\mathcal{X}}$
is a projective model of
 $X$
over
$X$
over
 $\mathbb{Z}_{p}$
, whose geometric special fiber is a K3 surface with RDP singularities of type
$\mathbb{Z}_{p}$
, whose geometric special fiber is a K3 surface with RDP singularities of type
 $A_{1}$
;
$A_{1}$
; -
(iii)
 $X$
has good reduction over the unramified extension
$X$
has good reduction over the unramified extension
 $\mathbb{Q}_{p}[\sqrt{c}]$
.
$\mathbb{Q}_{p}[\sqrt{c}]$
. -
(iv)
 $X$
does not have good reduction over
$X$
does not have good reduction over
 $\mathbb{Q}_{p}$
.
$\mathbb{Q}_{p}$
.
Proof. Smoothness of
![]() $X$
follows from considering the equations over
$X$
follows from considering the equations over
![]() $\mathbb{Z}$
, reducing modulo
$\mathbb{Z}$
, reducing modulo
![]() $2$
and checking smoothness there. Claims (ii) and (iii) are straightforward computations (for claim (iii), blow up the ideal
$2$
and checking smoothness there. Claims (ii) and (iii) are straightforward computations (for claim (iii), blow up the ideal
![]() ${\mathcal{I}}_{+}$
or
${\mathcal{I}}_{+}$
or
![]() ${\mathcal{I}}_{-}$
defined below), and, since
${\mathcal{I}}_{-}$
defined below), and, since
![]() $X$
has good reduction after an unramified extension, also claim (i) follows. We refer to [Reference MatsumotoMat15, §5.3] for computations and details.
$X$
has good reduction after an unramified extension, also claim (i) follows. We refer to [Reference MatsumotoMat15, §5.3] for computations and details.
To show claim (iv), we argue by contradiction, and assume that there exists a smooth and proper algebraic space
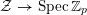 ${\mathcal{Z}}\rightarrow \operatorname{Spec}\mathbb{Z}_{p}$
with generic fiber
${\mathcal{Z}}\rightarrow \operatorname{Spec}\mathbb{Z}_{p}$
with generic fiber
![]() $X$
. Since the generic fibers of
$X$
. Since the generic fibers of
![]() ${\mathcal{X}}$
and
${\mathcal{X}}$
and
![]() ${\mathcal{Z}}$
are isomorphic, such an isomorphism extends to a birational, but possibly rational, map
${\mathcal{Z}}$
are isomorphic, such an isomorphism extends to a birational, but possibly rational, map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{Z}}{\dashrightarrow}{\mathcal{X}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:{\mathcal{Z}}{\dashrightarrow}{\mathcal{X}}.\end{eqnarray}$$
Next, let
![]() ${\mathcal{L}}$
be an ample invertible sheaf on
${\mathcal{L}}$
be an ample invertible sheaf on
![]() ${\mathcal{X}}$
, for example, the restriction of
${\mathcal{X}}$
, for example, the restriction of
![]() ${\mathcal{O}}(1)$
from the ambient
${\mathcal{O}}(1)$
from the ambient
![]() $\mathbb{P}_{\mathbb{Z}_{p}}^{3}$
. Restricting
$\mathbb{P}_{\mathbb{Z}_{p}}^{3}$
. Restricting
![]() ${\mathcal{L}}$
to the generic fiber
${\mathcal{L}}$
to the generic fiber
![]() ${\mathcal{X}}_{\unicode[STIX]{x1D702}}$
, and pulling it back via
${\mathcal{X}}_{\unicode[STIX]{x1D702}}$
, and pulling it back via
![]() $\unicode[STIX]{x1D6FC}$
, we obtain an ample invertible sheaf
$\unicode[STIX]{x1D6FC}$
, we obtain an ample invertible sheaf
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D702}}^{\ast }({\mathcal{L}}_{\unicode[STIX]{x1D702}})$
on
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D702}}^{\ast }({\mathcal{L}}_{\unicode[STIX]{x1D702}})$
on
![]() ${\mathcal{Z}}_{\unicode[STIX]{x1D702}}$
. Since
${\mathcal{Z}}_{\unicode[STIX]{x1D702}}$
. Since
![]() ${\mathcal{Z}}$
is smooth over
${\mathcal{Z}}$
is smooth over
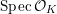 $\operatorname{Spec}{\mathcal{O}}_{K}$
, this invertible sheaf on
$\operatorname{Spec}{\mathcal{O}}_{K}$
, this invertible sheaf on
![]() ${\mathcal{Z}}_{\unicode[STIX]{x1D702}}$
extends uniquely to an invertible sheaf on
${\mathcal{Z}}_{\unicode[STIX]{x1D702}}$
extends uniquely to an invertible sheaf on
![]() ${\mathcal{Z}}$
that we denote by
${\mathcal{Z}}$
that we denote by
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
By Proposition 4.5, there exists a rational and birational map
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{Z}}{\dashrightarrow}{\mathcal{Z}}^{+},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:{\mathcal{Z}}{\dashrightarrow}{\mathcal{Z}}^{+},\end{eqnarray}$$
where
![]() ${\mathcal{Z}}^{+}$
is another model of
${\mathcal{Z}}^{+}$
is another model of
![]() $X$
with good reduction, and such that the transform
$X$
with good reduction, and such that the transform
![]() ${\mathcal{M}}^{+}$
of
${\mathcal{M}}^{+}$
of
![]() ${\mathcal{M}}$
on
${\mathcal{M}}$
on
![]() ${\mathcal{Z}}^{+}$
is ample on the generic fiber, and big and nef on the special fiber. We denote by
${\mathcal{Z}}^{+}$
is ample on the generic fiber, and big and nef on the special fiber. We denote by
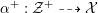 $\unicode[STIX]{x1D6FC}^{+}:{\mathcal{Z}}^{+}{\dashrightarrow}{\mathcal{X}}$
the composition
$\unicode[STIX]{x1D6FC}^{+}:{\mathcal{Z}}^{+}{\dashrightarrow}{\mathcal{X}}$
the composition
![]() $\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D711}^{-1}$
. Then
$\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D711}^{-1}$
. Then
 $$\begin{eqnarray}{\mathcal{Z}}^{+}\rightarrow ({\mathcal{Z}}^{+})^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{Z}}^{+},({\mathcal{M}}^{+})^{\otimes n})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}^{+}\rightarrow ({\mathcal{Z}}^{+})^{\prime }:=\operatorname{Proj}\bigoplus _{n\geqslant 0}H^{0}({\mathcal{Z}}^{+},({\mathcal{M}}^{+})^{\otimes n})\end{eqnarray}$$
is a birational morphism that contracts precisely those curves on the special fiber
![]() ${\mathcal{Z}}_{0}^{+}$
that have zero-intersection with
${\mathcal{Z}}_{0}^{+}$
that have zero-intersection with
![]() ${\mathcal{M}}_{0}^{+}$
, and nothing else. By construction, we have
${\mathcal{M}}_{0}^{+}$
, and nothing else. By construction, we have
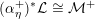 $(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D702}}^{+})^{\ast }{\mathcal{L}}\cong {\mathcal{M}}^{+}$
and thus, by [Reference KovacsKov09, Theorem 5.14], there exists an isomorphism
$(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D702}}^{+})^{\ast }{\mathcal{L}}\cong {\mathcal{M}}^{+}$
and thus, by [Reference KovacsKov09, Theorem 5.14], there exists an isomorphism
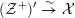 $({\mathcal{Z}}^{+})^{\prime }\stackrel{{\sim}}{\rightarrow }{\mathcal{X}}$
over
$({\mathcal{Z}}^{+})^{\prime }\stackrel{{\sim}}{\rightarrow }{\mathcal{X}}$
over
![]() $\operatorname{Spec}\mathbb{Z}_{p}$
.
$\operatorname{Spec}\mathbb{Z}_{p}$
.
Thus we have shown that the model
![]() ${\mathcal{X}}$
admits a simultaneous resolution
${\mathcal{X}}$
admits a simultaneous resolution
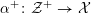 $\unicode[STIX]{x1D6FC}^{+}:{\mathcal{Z}}^{+}\rightarrow {\mathcal{X}}$
of singularities over
$\unicode[STIX]{x1D6FC}^{+}:{\mathcal{Z}}^{+}\rightarrow {\mathcal{X}}$
of singularities over
![]() $\mathbb{Z}_{p}$
. But then let
$\mathbb{Z}_{p}$
. But then let
![]() $x\in {\mathcal{X}}_{0}$
be an
$x\in {\mathcal{X}}_{0}$
be an
![]() $\mathbb{F}_{p}$
-rational singular point: for example, the point
$\mathbb{F}_{p}$
-rational singular point: for example, the point
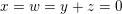 $x=w=y+z=0$
. Then let
$x=w=y+z=0$
. Then let
![]() ${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$
be the strict local ring, and denote by
${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$
be the strict local ring, and denote by
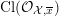 $\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
its Picard group. Then
$\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
its Picard group. Then
![]() $\unicode[STIX]{x1D6FC}^{+}$
induces a
$\unicode[STIX]{x1D6FC}^{+}$
induces a
![]() $G_{\mathbb{Q}_{p}}$
-equivariant surjection
$G_{\mathbb{Q}_{p}}$
-equivariant surjection
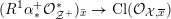 $(R^{1}\unicode[STIX]{x1D6FC}_{\ast }^{+}{\mathcal{O}}_{{\mathcal{Z}}^{+}}^{\ast })_{\bar{x}}\rightarrow \operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
. However, this is impossible for the following reasons.
$(R^{1}\unicode[STIX]{x1D6FC}_{\ast }^{+}{\mathcal{O}}_{{\mathcal{Z}}^{+}}^{\ast })_{\bar{x}}\rightarrow \operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
. However, this is impossible for the following reasons.
-
(i) The group
 $(R^{1}\unicode[STIX]{x1D6FC}_{\ast }^{+}{\mathcal{O}}_{{\mathcal{Z}}^{+}}^{\ast })_{\bar{x}}$
is generated by the class of the exceptional curve, which is
$(R^{1}\unicode[STIX]{x1D6FC}_{\ast }^{+}{\mathcal{O}}_{{\mathcal{Z}}^{+}}^{\ast })_{\bar{x}}$
is generated by the class of the exceptional curve, which is
 $\mathbb{F}_{p}$
-rational, and thus the
$\mathbb{F}_{p}$
-rational, and thus the
 $G_{\mathbb{Q}_{p}}$
-action on it is trivial.
$G_{\mathbb{Q}_{p}}$
-action on it is trivial. -
(ii) The
 $G_{\mathbb{Q}_{p}}$
-action on
$G_{\mathbb{Q}_{p}}$
-action on
 $\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
is non-trivial. More precisely, if we define the following ideals of
$\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
is non-trivial. More precisely, if we define the following ideals of
 ${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$
then their classes in
${\mathcal{O}}_{{\mathcal{X}},\overline{x}}$
then their classes in $$\begin{eqnarray}{\mathcal{I}}_{\pm }:=\biggl(w,\biggl(pz^{2}+xy+\frac{p}{2}yz\biggr)\pm \frac{\sqrt{c}}{2}pyz\biggr),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}_{\pm }:=\biggl(w,\biggl(pz^{2}+xy+\frac{p}{2}yz\biggr)\pm \frac{\sqrt{c}}{2}pyz\biggr),\end{eqnarray}$$
 $\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
satisfy
$\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
satisfy
 $[{\mathcal{I}}_{+}]=-[{\mathcal{I}}_{-}]\neq [{\mathcal{I}}_{-}]$
, and since
$[{\mathcal{I}}_{+}]=-[{\mathcal{I}}_{-}]\neq [{\mathcal{I}}_{-}]$
, and since
 $G_{\mathbb{Q}_{p}}$
acts on
$G_{\mathbb{Q}_{p}}$
acts on
 $\mathbb{Q}_{p}[\sqrt{c}]$
as
$\mathbb{Q}_{p}[\sqrt{c}]$
as
 $\sqrt{c}\mapsto -\sqrt{c}$
, the
$\sqrt{c}\mapsto -\sqrt{c}$
, the
 $G_{\mathbb{Q}_{p}}$
-action on
$G_{\mathbb{Q}_{p}}$
-action on
 $\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
is non-trivial.
$\operatorname{Cl}({\mathcal{O}}_{{\mathcal{X}},\overline{x}})$
is non-trivial.
This contradiction shows that
![]() $X$
does not have good reduction over
$X$
does not have good reduction over
![]() $\mathbb{Q}_{p}$
, and establishes claim (iv).◻
$\mathbb{Q}_{p}$
, and establishes claim (iv).◻
Remark 7.3. This example is the one the second named author gave in [Reference MatsumotoMat15, §5.3]. There, the choice of
![]() $\unicode[STIX]{x1D719}$
ensured that
$\unicode[STIX]{x1D719}$
ensured that
![]() $X$
was a smooth K3 surface, as well as of Picard number one. In the present paper, we only need smoothness, and therefore, could have used a simpler polynomial. The same remark holds for Example 5.4.
$X$
was a smooth K3 surface, as well as of Picard number one. In the present paper, we only need smoothness, and therefore, could have used a simpler polynomial. The same remark holds for Example 5.4.
Acknowledgements
It is a pleasure for us to thank François Charles, Christopher Hacon, Annabelle Hartmann, Brendan Hassett, Tetsushi Ito, Keerthi Madapusi Pera, Davesh Maulik, as well as Yoichi Mieda for discussions and comments. We also thank the referee for careful proofreading and many comments, including an idea to simplify the arguments in § 4.2. The second named author thanks the department of mathematics at the TU München for kind hospitality while visiting the first named author there.