It is proved that flatness of an analytic mapping germ from a complete intersection is determined by its sufficiently high jet. As a consequence, one obtains finite determinacy of complete intersections. It is also shown that flatness and openness are stable under deformations.

We obtain bounds for the number of variables required to establish Hasse principles, both for the existence of solutions and for asymptotic formulæ, for systems of additive equations containing forms of differing degree but also multiple forms of like degree. Apart from the very general estimates of Schmidt and Browning–Heath–Brown, which give weak results when specialized to the diagonal situation, this is the first result on such “hybrid” systems. We also obtain specialized results for systems of quadratic and cubic forms, where we are able to take advantage of some of the stronger methods available in that setting. In particular, we achieve essentially square root cancellation for systems consisting of one cubic and $r$ quadratic equations.

We study the regularity of convolution powers for measures supported on Salem sets, and prove related results on Fourier restriction and Fourier multipliers. In particular we show that for $\alpha $ of the form $d\,/\,n,\,n\,=\,2,3,...$ there exist $\alpha $-Salem measures for which the ${{L}^{2}}$ Fourier restriction theorem holds in the range $p\,\le \,\frac{2d}{2d\,-\,\alpha }$. The results rely on ideas of Körner. We extend some of his constructions to obtain upper regular $\alpha $-Salem measures, with sharp regularity results for $n$-fold convolutions for all $n\,\in \,\mathbb{N}$.

By a tiling of a topological linear space $X$, we mean a covering of $X$ by at least two closed convex sets, called tiles, whose nonempty interiors are pairwise disjoint. Study of tilings of infinite dimensional spaces was initiated in the 1980's with pioneer papers by V. Klee. We prove some general properties of tilings of locally convex spaces, and then apply these results to study the existence of tilings of normed and Banach spaces by tiles possessing certain smoothness or rotundity properties. For a Banach space $X$, our main results are the following.

• (i) $X$ admits no tiling by Fréchet smooth bounded tiles.

• (ii) If $X$ is locally uniformly rotund $\left( \text{LUR} \right)$, it does not admit any tiling by balls.

• (iii) On the other hand, some ${{\ell }_{1}}\left( \Gamma \right)$ spaces, $\Gamma $ uncountable, do admit a tiling by pairwise disjoint $\text{LUR}$ bounded tiles.

The aim of this paper is to prove that a $\text{K3}$ surface is the minimal model of the quotient of an Abelian surface by a group $G$ (respectively of a $\text{K3}$ surface by an Abelian group $G$) if and only if a certain lattice is primitively embedded in its Néron-Severi group. This allows one to describe the coarse moduli space of the $\text{K3}$ surfaces that are (rationally) $G$-covered by Abelian or $\text{K3}$ surfaces (in the latter case $G$ is an Abelian group). When $G$ has order 2 or $G$ is cyclic and acts on an Abelian surface, this result is already known; we extend it to the other cases.

Moreover, we prove that a $\text{K3}$ surface ${{X}_{G}}$ is the minimal model of the quotient of an Abelian surface by a group $G$ if and only if a certain configuration of rational curves is present on ${{X}_{G}}$. Again, this result was known only in some special cases, in particular, if $G$ has order 2 or 3.

Main result: If a ${{C}^{*}}$-algebra $\mathcal{A}$ is simple, $\sigma $-unital, has finitely many extremal traces, and has strict comparison of positive elements by traces, then its multiplier algebra $\mathcal{M}\left( \mathcal{A} \right)$ also has strict comparison of positive elements by traces. The same results holds if finitely many extremal traces is replaced by quasicontinuous scale. A key ingredient in the proof is that every positive element in the multiplier algebra of an arbitrary $\sigma $-unital ${{C}^{*}}$ -algebra can be approximated by a bi-diagonal series. As an application of strict comparison, if $\mathcal{A}$ is a simple separable stable ${{C}^{*}}$ -algebra with real rank zero, stable rank one, and strict comparison of positive elements by traces, then whether a positive element is a positive linear combination of projections is determined by the trace values of its range projection.

This paper concerns free function theory. Free maps are free analogs of analytic functions in several complex variables and are defined in terms of freely noncommuting variables. A function of $g$ noncommuting variables is a function on $g$-tuples of square matrices of all sizes that respects direct sums and simultaneous conjugation. Examples of such maps include noncommutative polynomials, noncommutative rational functions, and convergent noncommutative power series.

In sharp contrast to the existing literature in free analysis, this article investigates free maps with involution, free analogs of real analytic functions. To get a grip on these, techniques and tools from invariant theory are developed and applied to free analysis. Here is a sample of the results obtained. A characterization of polynomial free maps via properties of their finite-dimensional slices is presented and then used to establish power series expansions for analytic free maps about scalar and non-scalar points; the latter are series of generalized polynomials for which an invariant-theoretic characterization is given. Furthermore, an inverse and implicit function theorem for free maps with involution is obtained. Finally, with a selection of carefully chosen examples it is shown that free maps with involution do not exhibit strong rigidity properties enjoyed by their involution-free counterparts.

In this paper we introduce a new way of deforming convolution algebras and Fourier algebras on locally compact groups. We demonstrate that this new deformation allows us to reveal some information about the underlying groups by examining Banach algebra properties of deformed algebras. More precisely, we focus on representability as an operator algebra of deformed convolution algebras on compact connected Lie groups with connection to the real dimension of the underlying group. Similarly, we investigate complete representability as an operator algebra of deformed Fourier algebras on some finitely generated discrete groups with connection to the growth rate of the group.

The closest infinite-dimensional relatives of compact Lie algebras are Hilbert-Lie algebras, i.e., real Hilbert spaces with a Lie algebra structure for which the scalar product is invariant. Locally affine Lie algebras 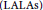$\left( \text{LALAs} \right)$ correspond to double extensions of (twisted) loop algebras over simple Hilbert-Lie algebras $\mathfrak{k}$, also called affinisations of $\mathfrak{k}$. They possess a root space decomposition whose corresponding root system is a locally affine root system of one of the 7 families

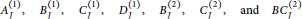$$A_{J}^{\left( 1 \right)},\,B_{J}^{\left( 1 \right)},\,C_{J}^{\left( 1 \right)},\,D_{J}^{\left( 1 \right)},\,B_{J}^{\left( 2 \right)},\,C_{J}^{\left( 2 \right)},\,\,\text{and}\,BC_{J}^{\left( 2 \right)}$$

for some infinite set 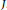$J$. To each of these types corresponds a “minimal ” affinisation of some simple Hilbert-Lie algebra $\mathfrak{k}$, which we call standard.

In this paper, we give for each affinisation $\mathfrak{g}$ of a simple Hilbert-Lie algebra $\mathfrak{k}$ an explicit isomorphism from $\mathfrak{g}$ to one of the standard affinisations of $\mathfrak{k}$. The existence of such an isomorphism could also be derived from the classiffication of locally affine root systems, but for representation theoretic purposes it is crucial to obtain it explicitly as a deformation between two twists that is compatible with the root decompositions. We illustrate this by applying our isomorphism theorem to the study of positive energy highest weight representations of $\mathfrak{g}$. In subsequent work, this paper will be used to obtain a complete classification of the positive energy highest weight representations of affinisations of $\mathfrak{k}$.