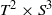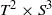1 results
Extremal Sasakian geometry on
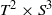 ${T}^{2} \times {S}^{3} $ and related manifolds
${T}^{2} \times {S}^{3} $ and related manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1431-1456
- Print publication:
- August 2013
-
- Article
- Export citation