1 results
Paschke's conjecture for the endpoint anisotropic series representations of the free group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 173-184
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation

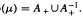 . Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ
. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ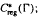 in particular, Paschke's conjecture holds for λ − μ.
in particular, Paschke's conjecture holds for λ − μ.