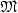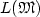1 results
Decidability of code properties
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 41 / Issue 3 / July 2007
- Published online by Cambridge University Press:
- 25 September 2007, pp. 243-259
- Print publication:
- July 2007
-
- Article
- Export citation