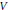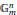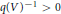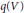2 results
Petits points d’une surface
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 5 / 01 October 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1118-1150
- Print publication:
- 01 October 2009
-
- Article
-
- You have access
- Export citation
MINORATION DE LA HAUTEUR NORMALISÉE DANS UN TORE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 2 / Issue 3 / July 2003
- Published online by Cambridge University Press:
- 21 July 2003, pp. 335-381
- Print publication:
- July 2003
-
- Article
- Export citation