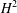1 results
NEW GLOBAL LOGARITHMIC STABILITY RESULTS ON THE CAUCHY PROBLEM FOR ELLIPTIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 141-145
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation