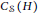2 results
Classification of Simple Weight Modules over the Schrödinger Algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-39
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
On Global Dimensions of Tree Type Finite Dimensional Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 814-820
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation