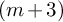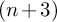Several structural results about permutation groups of finite rank definable in differentially closed fields of characteristic zero (and other similar theories) are obtained. In particular, it is shown that every finite rank definably primitive permutation group is definably isomorphic to an algebraic permutation group living in the constants. Applications include the verification, in differentially closed fields, of the finite Morley rank permutation group conjectures of Borovik-Deloro and Borovik-Cherlin. Applying the results to binding groups for internality to the constants, it is deduced that if complete types p and q are of rank m and n, respectively, and are nonorthogonal, then the 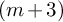 $(m+3)$rd Morley power of p is not weakly orthogonal to the
$(m+3)$rd Morley power of p is not weakly orthogonal to the 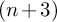 $(n+3)$rd Morley power of q. An application to transcendence of generic solutions of pairs of algebraic differential equations is given.
$(n+3)$rd Morley power of q. An application to transcendence of generic solutions of pairs of algebraic differential equations is given.