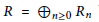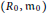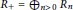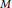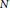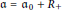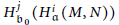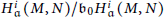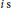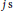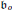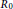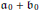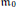Let
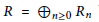 $R\,=\,{{\oplus }_{n\ge 0}}{{R}_{n}}$
be a graded Noetherian ring with local base ring
$R\,=\,{{\oplus }_{n\ge 0}}{{R}_{n}}$
be a graded Noetherian ring with local base ring
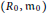 $\left( {{R}_{0}},{{\text{m}}_{0}} \right)$
and let
$\left( {{R}_{0}},{{\text{m}}_{0}} \right)$
and let
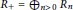 ${{R}_{+}}\,=\,{{\oplus }_{n>0}}{{R}_{n}}$
. Let
${{R}_{+}}\,=\,{{\oplus }_{n>0}}{{R}_{n}}$
. Let
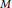 $M$
and
$M$
and
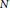 $N$
be finitely generated graded
$N$
be finitely generated graded
 $R$
-modules and let
$R$
-modules and let
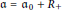 $\mathfrak{a}\,=\,{{\mathfrak{a}}_{0}}\,+\,{{R}_{+}}$
an ideal of
$\mathfrak{a}\,=\,{{\mathfrak{a}}_{0}}\,+\,{{R}_{+}}$
an ideal of
 $R$
. We show that
$R$
. We show that
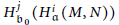 $H_{\mathfrak{b}0}^{j}\,\left( H_{\mathfrak{a}}^{i}\left( M,\,N \right) \right)$
and
$H_{\mathfrak{b}0}^{j}\,\left( H_{\mathfrak{a}}^{i}\left( M,\,N \right) \right)$
and
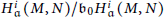 ${H_{\mathfrak{a}}^{i}\left( M,\,N \right)}/{{{\mathfrak{b}}_{0}}H_{\mathfrak{a}}^{i}\left( M,\,N \right)}\;$
are Artinian for some
${H_{\mathfrak{a}}^{i}\left( M,\,N \right)}/{{{\mathfrak{b}}_{0}}H_{\mathfrak{a}}^{i}\left( M,\,N \right)}\;$
are Artinian for some
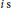 $i\text{ s}$
and
$i\text{ s}$
and
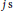 $j\,\text{s}$
with a specified property, where
$j\,\text{s}$
with a specified property, where
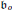 ${{\mathfrak{b}}_{o}}$
is an ideal of
${{\mathfrak{b}}_{o}}$
is an ideal of
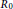 ${{R}_{0}}$
such that
${{R}_{0}}$
such that
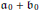 ${{\mathfrak{a}}_{0}}\,+\,{{\mathfrak{b}}_{0}}$
is an
${{\mathfrak{a}}_{0}}\,+\,{{\mathfrak{b}}_{0}}$
is an
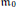 ${{\mathfrak{m}}_{0}}$
-primary ideal.
${{\mathfrak{m}}_{0}}$
-primary ideal.