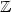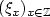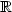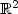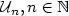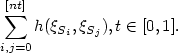1 results
Limit theorems for U-statistics indexed by a onedimensional random walk
-
- Journal:
- ESAIM: Probability and Statistics / Volume 9 / February 2005
- Published online by Cambridge University Press:
- 15 November 2005, pp. 98-115
- Print publication:
- February 2005
-
- Article
- Export citation
-
Let (Sn)n≥0 be a $\mathbb Z$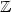
-random walk and $(\xi_{x})_{x\in \mathbb Z}$ 
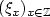be a sequence of independent andidentically distributed $\mathbb R$ 
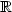-valued random variables,independent of the random walk. Let h be a measurable, symmetricfunction defined on $\mathbb R^2$ 
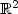with values in $\mathbb R$ 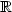. We study theweak convergence of the sequence ${\cal U}_{n}, n\in \mathbb N$ 
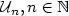, withvalues in D[0,1] the set of right continuous real-valuedfunctions with left limits, defined by \[ \sum_{i,j=0}^{[nt]}h(\xi_{S_{i}},\xi_{S_{j}}), t\in[0,1].\] 
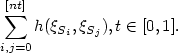Statistical applications are presented, in particular we prove a strong law of large numbersfor U-statistics indexed by a one-dimensional random walk using a result of [1].
