n candidates, represented by n i.i.d. continuous random variables X1, …, Xn with known distribution arrive sequentially, and one of them must be chosen, using a non-anticipating stopping rule. The objective is to minimize the expected rank (among the ranks of X1, …, Xn) of the candidate chosen, where the best candidate, i.e. the one with smallest X-value, has rank one, etc. Let the value of the optimal rule be Vn, and lim Vn = V. We prove that V > 1.85. Limiting consideration to the class of threshold rules of the form tn = min {k: Xk ≦ ak for some constants ak, let Wn be the value of the expected rank for the optimal threshold rule, and lim Wn = W. We show 2.295 < W < 2.327.
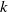 $k$-out-of-
$k$-out-of- $n$ systems with discrete distributions
$n$ systems with discrete distributions