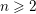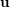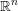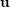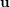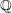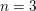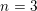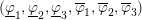Fix an integer 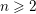$n\geqslant 2$. To each non-zero point 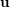$\mathbf{u}$ in 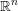$\mathbb{R}^{n}$, one attaches several numbers called exponents of Diophantine approximation. However, as Khintchine first observed, these numbers are not independent of each other. This raises the problem of describing the set of all possible values that a given family of exponents can take by varying the point 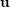$\mathbf{u}$. To avoid trivialities, one restricts to points 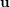$\mathbf{u}$ whose coordinates are linearly independent over 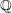$\mathbb{Q}$. The resulting set of values is called the spectrum of these exponents. We show that, in an appropriate setting, any such spectrum is a compact connected set. In the case 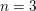$n=3$, we prove moreover that it is a semi-algebraic set closed under component-wise minimum. For 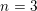$n=3$, we also obtain a description of the spectrum of the exponents 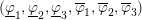$(\text{}\underline{\unicode[STIX]{x1D711}}_{1},\text{}\underline{\unicode[STIX]{x1D711}}_{2},\text{}\underline{\unicode[STIX]{x1D711}}_{3},\overline{\unicode[STIX]{x1D711}}_{1},\overline{\unicode[STIX]{x1D711}}_{2},\overline{\unicode[STIX]{x1D711}}_{3})$ recently introduced by Schmidt and Summerer.