1 results
A relative of the approachability ideal, diamond and non-saturation
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1035-1065
- Print publication:
- September 2010
-
- Article
- Export citation
-
Let λ denote a singular cardinal. Zeman, improving a previous result of Shelah, proved that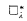
together with 2λ = λ+ implies ⋄S for every S ⊆ λ+ that reflects stationarily often.In this paper, for a set S ⊆ λ+, a normal subideal of the weak approachability ideal is introduced, and denoted by I[S; λ]. We say that the ideal is fat if it contains a stationary set. It is proved:
1. if I[S; λ] is fat, then NSλ + ∣ S is non-saturated;
2. if I[S; λ] is fat and 2λ = λ+, then ⋄S holds;
3.
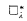implies that I[S; λ] is fat for every S ⊆ λ+ that reflects stationarily often;4. it is relatively consistent with the existence of a supercompact cardinal that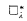
fails, while I[S; λ] is fat for every stationary S ⊆ λ+ that reflects stationarily often.The stronger principle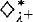
is studied as well.
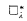together with 2
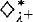is studied as well.