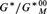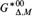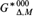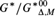For a group G definable in a first order structure M we develop basic topological dynamics in the category of definable G-flows. In particular, we give a description of the universal definable G-ambit and of the semigroup operation on it. We find a natural epimorphism from the Ellis group of this flow to the definable Bohr compactification of G, that is to the quotient 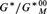 ${G^{\rm{*}}}/G_M^{{\rm{*}}00}$ (where G* is the interpretation of G in a monster model). More generally, we obtain these results locally, i.e., in the category of Δ-definable G-flows for any fixed set Δ of formulas of an appropriate form. In particular, we define local connected components
${G^{\rm{*}}}/G_M^{{\rm{*}}00}$ (where G* is the interpretation of G in a monster model). More generally, we obtain these results locally, i.e., in the category of Δ-definable G-flows for any fixed set Δ of formulas of an appropriate form. In particular, we define local connected components 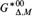 $G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ and
$G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ and 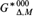 $G_{{\rm{\Delta }},M}^{{\rm{*}}000}$, and show that
$G_{{\rm{\Delta }},M}^{{\rm{*}}000}$, and show that 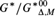 ${G^{\rm{*}}}/G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ is the Δ-definable Bohr compactification of G. We also note that some deeper arguments from [14] can be adapted to our context, showing for example that our epimorphism from the Ellis group to the Δ-definable Bohr compactification factors naturally yielding a continuous epimorphism from the Δ-definable generalized Bohr compactification to the Δ-definable Bohr compactification of G. Finally, we propose to view certain topological-dynamic and model-theoretic invariants as Polish structures which leads to some observations and questions.
${G^{\rm{*}}}/G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ is the Δ-definable Bohr compactification of G. We also note that some deeper arguments from [14] can be adapted to our context, showing for example that our epimorphism from the Ellis group to the Δ-definable Bohr compactification factors naturally yielding a continuous epimorphism from the Δ-definable generalized Bohr compactification to the Δ-definable Bohr compactification of G. Finally, we propose to view certain topological-dynamic and model-theoretic invariants as Polish structures which leads to some observations and questions.