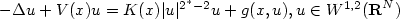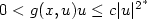In this paper we establish a variant and generalized weak linking theorem, which contains more delicate result and insures the existence of bounded Palais–Smale sequences of a strongly indefinite functional. The abstract result will be used to study the semilinear Schrödinger equation $-\Delta u+V(x)u=K(x)|u|^{2^\ast-2}u+g(x, u), u\in W^{1,2}({\bf R}^N)$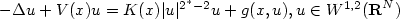, where N ≥ 4; V,K,g are periodic in xj for 1 ≤ j ≤ N and 0 is in a gap of the spectrum of -Δ + V; K>0. 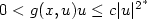If $0<g(x, u)u\leq c|u|^{2^\ast}$ for an appropriate constant c, we show that this equation has a nontrivial solution.