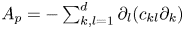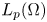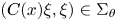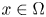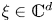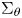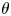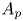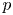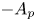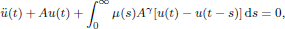2 results
On sectoriality of degenerate elliptic operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 18 August 2021, pp. 689-710
-
- Article
- Export citation
The lack of exponential stability for a class of second-order systems with memory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 683-702
- Print publication:
- August 2017
-
- Article
- Export citation