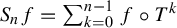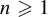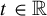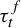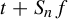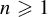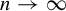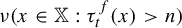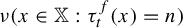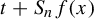1 results
Conditioned limit theorems for hyperbolic dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 50-117
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation