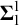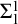We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the bi-embeddability and elementary bi-embeddability relation on graphs under Borel reducibility and investigate the degree spectra realized by these relations. We first give a Borel reduction from embeddability on graphs to elementary embeddability on graphs. As a consequence we obtain that elementary bi-embeddability on graphs is a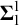 
$\boldsymbol {\Sigma }^1_1$
complete equivalence relation. We then investigate the algorithmic properties of this reduction. We obtain that elementary bi-embeddability on the class of computable graphs is 
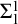$\Sigma ^1_1$
complete with respect to computable reducibility and show that the elementary bi-embeddability and bi-embeddability spectra realized by graphs are related.
