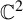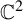1 results
Topological and geometric hyperbolicity criteria for polynomial automorphisms of
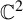 ${\mathbb {C}^2}$
${\mathbb {C}^2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2151-2171
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation