2 results
Commuting Varieties for Nilpotent Radicals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 559-594
-
- Article
- Export citation
On Commuting Varieties of Nilradicals of Borel Subalgebras of Reductive Lie Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 169-181
-
- Article
-
- You have access
- Export citation

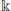 of characteristic 0. We consider the commuting variety
of characteristic 0. We consider the commuting variety 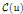 of the nilradical
of the nilradical 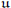 of the Lie algebra
of the Lie algebra 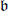 of a Borel subgroup
of a Borel subgroup 