In this paper we study with proof-theoretic methods the function(al)s provably recursive relative to Ramsey's theorem for pairs and the cohesive principle (COH).

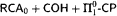Our main result on COH is that the type 2 functional provably recursive from are primitive recursive. This also provides a uniform method to extract bounds from proofs that use these principles. As a consequence we obtain a new proof of the fact that 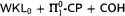is 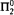-conservative over PRA.

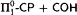Recent work of the first author showed that is equivalent to a weak variant of the Bolzano-Weierstraß principle. This makes it possible to use our results to analyze not only combinatorial but also analytical proofs.

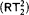For Ramsey's theorem for pairs and two colors we obtain the upper bounded that the type 2 functional provable recursive relative to 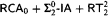are in 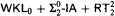T1. This is the fragment of Gödel's system T containing only type 1 recursion—roughly speaking it consists of functions of Ackermann type. With this we also obtain a uniform method for the extraction of T1-bounds from proofs that use . Moreover, this yields a new proof of the fact that is 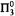-conservative over .

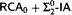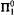The results are obtained in two steps: in the first step a term including Skolem functions for the above principles is extracted from a given proof. This is done using Gödel's functional interpretation. After this the term is normalized, such that only specific instances of the Skolem functions are used. In the second step this term is interpreted using -comprehension. The comprehension is then eliminated in favor of induction using either elimination of monotone Skolem functions (for COH) or Howard's ordinal analysis of bar recursion (for ).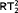