We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let I be a set and let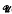 
(I) denote the set consisting of the 0 matrix over I × I and the matrix units over I × I. Then for x, z in 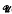(I) and x≠0≠z, xyz≠0 has precisely one solution y. This and several other statements are shown to be equivalent characterizations of 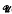(I) regarded as a semigroup with zero.
1980 Mathematics subject classification (Amer. Math. Soc.): 20 M 10.
