Let B be a superatomic Boolean algebra (BA). The rank of B (rk(B)). is defined to be the Cantor Bendixon rank of the Stone space of B. If a ∈ B − {0}, then the rank of a in B (rk(a)). is defined to be the rank of the Boolean algebra 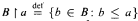. The rank of 0B is defined to be −1. An element a ∈ B − {0} is a generalized atom 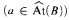, if the last nonzero cardinal in the cardinal sequence of B ↾ a is 1. Let a, b ∈ . We denote a ˜ b, if rk(a) = rk(b) = rk(a · b). A subset H ⊆ is a complete set of representatives (CSR) for B, if for every a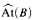 there is a unique h ∈ H such that h ~ a. Any CSR for B generates B. We say that B is canonically well-generated (CWG), if it has a CSR H such that the sublattice of B generated by H is well-founded. We say that B is well-generated, if it has a well-founded sublattice L such that L generates B.

Theorem 1. Let B be a Boolean algebra with cardinal sequence 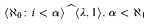. If B is CWG, then every subalgebra of B is CWG.

A superatomic Boolean algebra B is essentially low (ESL), if it has a countable ideal I such that rk(B/I) ≤ 1.

Theorem 1 follows from Theorem 2.9. which is the main result of this work. For an ESL BA B we define a set FB of partial functions from a certain countably infinite set to ω (Definition 2.8). Theorem 2.9 says that if B is an ESL Boolean algebra, then the following are equivalent.

(1) Every subalgebra of B is CWG: and

(2) FB is bounded.

Theorem 2. If an ESL Boolean algebra is not CWG, then it has a subalgebra which is not well-generated.