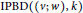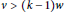4 results
3 - Laplacian eigenvalues and optimality
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 176-265
-
- Chapter
- Export citation
An Existence Theory for Incomplete Designs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 287-302
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Daisy structure in Desarguesian projective planes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-154
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
Configural errors on WISC–III block design
-
- Journal:
- Journal of the International Neuropsychological Society / Volume 5 / Issue 6 / September 1999
- Published online by Cambridge University Press:
- 01 September 1999, pp. 518-524
-
- Article
- Export citation