Let 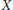 X and
X and 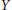 Y be metric spaces and
Y be metric spaces and 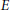 E,
E, 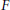 F be Banach spaces. Suppose that both
F be Banach spaces. Suppose that both 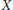 X and
X and 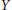 Y are realcompact, or both
Y are realcompact, or both 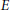 E,
E, 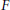 F are realcompact. The zero set of a vector-valued function
F are realcompact. The zero set of a vector-valued function 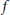 f is denoted by
f is denoted by 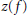 z\left( f \right). A linear bijection
z\left( f \right). A linear bijection 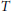 T between local or generalized Lipschitz vector-valued function spaces is said to preserve zero-set containments or nonvanishing functions if
T between local or generalized Lipschitz vector-valued function spaces is said to preserve zero-set containments or nonvanishing functions if
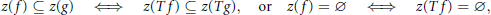 z\left( f \right)\,\subseteq \,z\left( g \right)\,\,\,\,\Leftrightarrow \,\,\,\,z\left( Tf \right)\,\subseteq \,z\left( Tg \right),\,\,\,\,\,\text{or}\,\,\,\,z\left( f \right)\,=\,\varnothing \,\,\,\Leftrightarrow \,\,\,z\left( Tf \right)\,=\,\varnothing ,
z\left( f \right)\,\subseteq \,z\left( g \right)\,\,\,\,\Leftrightarrow \,\,\,\,z\left( Tf \right)\,\subseteq \,z\left( Tg \right),\,\,\,\,\,\text{or}\,\,\,\,z\left( f \right)\,=\,\varnothing \,\,\,\Leftrightarrow \,\,\,z\left( Tf \right)\,=\,\varnothing ,respectively. Every zero-set containment preserver, and every nonvanishing function preserver when
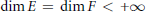 \dim\,E\,=\,\dim\,F\,<\,+\infty, is a weighted composition operator
\dim\,E\,=\,\dim\,F\,<\,+\infty, is a weighted composition operator 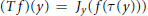 \left( Tf \right)\left( y \right)\,=\,{{J}_{y}}\left( f\left( \tau \left( y \right) \right) \right). We show that the map
\left( Tf \right)\left( y \right)\,=\,{{J}_{y}}\left( f\left( \tau \left( y \right) \right) \right). We show that the map 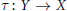 \tau \,:\,Y\,\to \,X is a locally (little) Lipschitz homeomorphism.
\tau \,:\,Y\,\to \,X is a locally (little) Lipschitz homeomorphism.