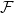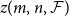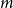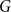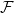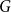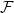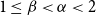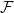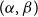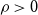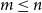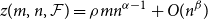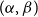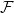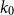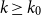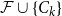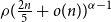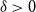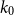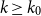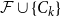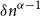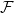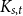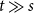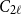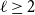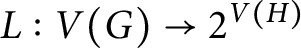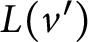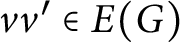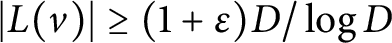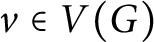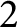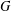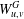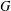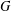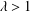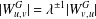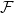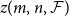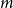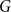Given a family $\mathcal{F}$ of bipartite graphs, the Zarankiewicz number $z(m,n,\mathcal{F})$ is the maximum number of edges in an $m$ by $n$ bipartite graph $G$ that does not contain any member of 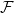$\mathcal{F}$ as a subgraph (such 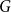$G$ is called 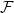$\mathcal{F}$ -free). For 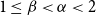$1\leq \beta \lt \alpha \lt 2$ , a family 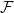$\mathcal{F}$ of bipartite graphs is 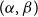$(\alpha,\beta )$ -smooth if for some 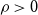$\rho \gt 0$ and every 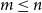$m\leq n$ , 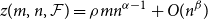$z(m,n,\mathcal{F})=\rho m n^{\alpha -1}+O(n^\beta )$ . 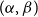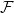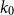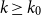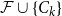Motivated by their work on a conjecture of Erdős and Simonovits on compactness and a classic result of Andrásfai, Erdős and Sós, Allen, Keevash, Sudakov and Verstraëte proved that for any $(\alpha,\beta )$ -smooth family $\mathcal{F}$ , there exists $k_0$ such that for all odd $k\geq k_0$ and sufficiently large $n$ , any $n$ -vertex $\mathcal{F}\cup \{C_k\}$ -free graph with minimum degree at least 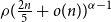$\rho (\frac{2n}{5}+o(n))^{\alpha -1}$ is bipartite. 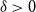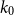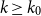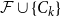In this paper, we strengthen their result by showing that for every real $\delta \gt 0$ , there exists $k_0$ such that for all odd $k\geq k_0$ and sufficiently large $n$ , any $n$ -vertex $\mathcal{F}\cup \{C_k\}$ -free graph with minimum degree at least 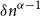$\delta n^{\alpha -1}$ is bipartite. Furthermore, our result holds under a more relaxed notion of smoothness, which include the families 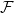$\mathcal{F}$ consisting of the single graph 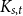$K_{s,t}$ when 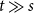$t\gg s$ . We also prove an analogous result for 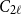$C_{2\ell }$ -free graphs for every 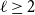$\ell \geq 2$ , which complements a result of Keevash, Sudakov and Verstraëte.

Suppose G and H are bipartite graphs and $L: V(G)\to 2^{V(H)}$ induces a partition of $V(H)$ such that the subgraph of H induced between $L(v)$ and $L(v')$ is a matching, whenever $vv'\in E(G)$ . We show for each $\varepsilon>0$ that if H has maximum degree D and $|L(v)| \ge (1+\varepsilon )D/\log D$ for all $v\in V(G)$ , then H admits an independent transversal with respect to L, provided D is sufficiently large. This bound on the part sizes is asymptotically sharp up to a factor $2$ . We also show some asymmetric variants of this result.

We study the theory Tm,n of existentially closed incidence structures omitting the complete incidence structure Km,n, which can also be viewed as existentially closed Km,n-free bipartite graphs. In the case m = n = 2, this is the theory of existentially closed projective planes. We give an $\forall \exists$-axiomatization of Tm,n, show that Tm,n does not have a countable saturated model when m, n ≥ 2, and show that the existence of a prime model for T2,2 is equivalent to a longstanding open question about finite projective planes. Finally, we analyze model theoretic notions of complexity for Tm,n. We show that Tm,n is NSOP1, but not simple when m, n ≥ 2, and we show that Tm,n has weak elimination of imaginaries but not full elimination of imaginaries. These results rely on combinatorial characterizations of various notions of independence, including algebraic independence, Kim independence, and forking independence.

For an edge $uv$ in a graph $G$, $W_{u,v}^{G}$ denotes the set of all vertices of $G$ that are closer to $u$ than to $v$. A graph $G$ is said to be quasi-distance-balanced if there exists a constant $\unicode[STIX]{x1D706}>1$ such that $|W_{u,v}^{G}|=\unicode[STIX]{x1D706}^{\pm 1}|W_{v,u}^{G}|$ for every pair of adjacent vertices $u$ and $v$. The existence of nonbipartite quasi-distance-balanced graphs is an open problem. In this paper we investigate the possible structure of cycles in quasi-distance-balanced graphs and generalise the previously known result that every quasi-distance-balanced graph is triangle-free. We also prove that a connected quasi-distance-balanced graph admitting a bridge is isomorphic to a star. Several open problems are posed.

A hypergraph is Helly if every family of hyperedges of it, formed by pairwiseintersecting hyperedges, has a common vertex. We consider the concepts ofbipartite-conformal and (colored) bipartite-Helly hypergraphs. In the same way asconformal hypergraphs and Helly hypergraphs are dual concepts, bipartite-conformal andbipartite-Helly hypergraphs are also dual. They are useful for characterizing bicliquematrices and biclique graphs, that is, the incident biclique-vertex incidence matrix andthe intersection graphs of the maximal bicliques of a graph, respectively. These conceptsplay a similar role for the bicliques of a graph, as do clique matrices and clique graphs,for the cliques of the graph. We describe polynomial time algorithms for recognizingbipartite-conformal and bipartite-Helly hypergraphs as well as biclique matrices.

In this note, we strengthen the inapproximation bound of O(logn) for the labeled perfect matching problem established in J.Monnot, The Labeled perfect matching in bipartite graphs, Information Processing Letters96 (2005) 81–88, using aself improving operation in some hard instances. It is interestingto note that this self improving operation does not work for allinstances. Moreover, based on this approach we deduce that theproblem does not admit constant approximation algorithms forconnected planar cubic bipartite graphs.