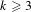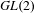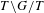We finalize the analysis of the trace formula initiated in S. A. Altuğ [Beyond endoscopy via the trace formula-I: Poisson summation and isolation of special representations, Compos. Math.151(10) (2015), 1791–1820] and developed in S. A. Altuğ [Beyond endoscopy via the trace formula-II: asymptotic expansions of Fourier transforms and bounds toward the Ramanujan conjecture. 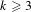Submitted, preprint, 2015, Available at: arXiv:1506.08911.pdf], and calculate the asymptotic expansion of the beyond endoscopic averages for the standard $L$-functions attached to weight $k\geqslant 3$ cusp forms on 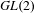$\mathit{GL}(2)$ (cf. Theorem 1.1). This, in particular, constitutes the first example of beyond endoscopy executed via the Arthur–Selberg trace formula, as originally proposed in R. P. Langlands [Beyond endoscopy, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 611–698 (The Johns Hopkins University Press, Baltimore, MD, 2004), chapter 22]. As an application we also give a new proof of the analytic continuation of the $L$-function attached to Ramanujan’s 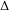$\unicode[STIX]{x1D6E5}$-function.

For the group $G=\operatorname{PGL}_{2}$ we perform a comparison between two relative trace formulas: on the one hand, the relative trace formula of Jacquet for the quotient $T\backslash G/T$, where $T$ is a nontrivial torus, and on the other the Kuznetsov trace formula (involving Whittaker periods), applied to nonstandard test functions. This gives a new proof of the celebrated result of Waldspurger on toric periods, and suggests a new way of comparing trace formulas, with some analogies to Langlands’ ‘Beyond Endoscopy’ program.

With analytic applications in mind, in particular beyond endoscopy, we initiate the study of the elliptic part of the trace formula. Incorporating the approximate functional equation into the elliptic part, we control the analytic behavior of the volumes of tori that appear in the elliptic part. Furthermore, by carefully choosing the truncation parameter in the approximate functional equation, we smooth out the singularities of orbital integrals. Finally, by an application of Poisson summation we rewrite the elliptic part so that it is ready to be used in analytic applications, and in particular in beyond endoscopy. As a by product we also isolate the contributions of special representations as pointed out in [Beyond endoscopy, in Contributions to automorphic forms, geometry and number theory (Johns Hopkins University Press, Baltimore, MD, 2004), 611–697].