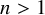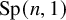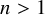For any $n>1$ we determine the uniform and nonuniform lattices of the smallest covolume in the Lie group $\operatorname {\mathrm {Sp}}(n,1)$ . We explicitly describe them in terms of the ring of Hurwitz integers in the nonuniform case with n even, respectively, of the icosian ring in the uniform case for all $n>1$ .

let g be an algebraic group, $\gamma$ an arithmetic lattice of g and $x=\gamma\backslash g$. if h is an algebraic subgroup of g such that $h\cap \gamma$ is a lattice of h, then $\gamma\backslash \gamma h\subset x$ is endowed with a canonical h-invariant probability measure $\mu_h$. using ratner's theory, we give general examples where $\mu_{h_n}$ converges weakly to $\mu_g$ if hn is a strict sequence of algebraic subgroups of g. if $\gamma$ is a congruence subgroup of g, we define another probability measure $\mu_h^a$ on x by using the adelic description of the quotient. we conjecture that $\mu_{h_n}^a$ always converges weakly to $\mu_g$ if hn is a strict sequence. using automorphic forms and l-functions, we describe the case $g=\textit{sl}(2,f)$ for a number field f and a sequence of tori hn. the relation with similar problems on shimura varieties is explained.