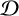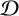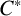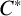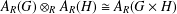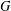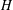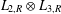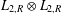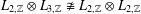The complex algebra of an inverse semigroup with finitely many idempotents in each \mathcal D$\mathcal D$-class is stably finite by a result of Munn. This can be proved fairly easily using C^{*}$C^{*}$-algebras for inverse semigroups satisfying this condition that have a Hausdorff universal groupoid, or more generally for direct limits of inverse semigroups satisfying this condition and having Hausdorff universal groupoids. It is not difficult to see that a finitely presented inverse semigroup with a non-Hausdorff universal groupoid cannot be a direct limit of inverse semigroups with Hausdorff universal groupoids. We construct here countably many nonisomorphic finitely presented inverse semigroups with finitely many idempotents in each \mathcal D$\mathcal D$-class and non-Hausdorff universal groupoids. At this time, there is not a clear C^{*}$C^{*}$-algebraic technique to prove these inverse semigroups have stably finite complex algebras.

Twisted étale groupoid algebras have recently been studied in the algebraic setting by several authors in connection with an abstract theory of Cartan pairs of rings. In this paper we show that extensions of ample groupoids correspond in a precise manner to extensions of Boolean inverse semigroups. In particular, discrete twists over ample groupoids correspond to certain abelian extensions of Boolean inverse semigroups, and we show that they are classified by Lausch’s second cohomology group of an inverse semigroup. The cohomology group structure corresponds to the Baer sum operation on twists.

We also define a novel notion of inverse semigroup crossed product, generalizing skew inverse semigroup rings, and prove that twisted Steinberg algebras of Hausdorff ample groupoids are instances of inverse semigroup crossed products. The cocycle defining the crossed product is the same cocycle that classifies the twist in Lausch cohomology.

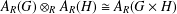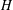We prove that A_{R}(G)\otimes _{R}A_{R}(H)\cong A_{R}(G\times H)$A_{R}(G)\otimes _{R}A_{R}(H)\cong A_{R}(G\times H)$ if G$G$ and H$H$ are Hausdorff ample groupoids. As part of the proof, we give a new universal property of Steinberg algebras. We then consider the isomorphism problem for tensor products of Leavitt algebras, and show that no diagonal-preserving isomorphism exists between 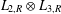L_{2,R}\otimes L_{3,R}$L_{2,R}\otimes L_{3,R}$ and 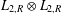L_{2,R}\otimes L_{2,R}$L_{2,R}\otimes L_{2,R}$. In fact, there are no unexpected diagonal-preserving isomorphisms between tensor products of finitely many Leavitt algebras. We give an easy proof that every \ast$\ast$-isomorphism of Steinberg algebras over the integers preserves the diagonal, and it follows that 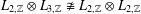L_{2,\mathbb{Z}}\otimes L_{3,\mathbb{Z}}\not \cong L_{2,\mathbb{Z}}\otimes L_{2,\mathbb{Z}}$L_{2,\mathbb{Z}}\otimes L_{3,\mathbb{Z}}\not \cong L_{2,\mathbb{Z}}\otimes L_{2,\mathbb{Z}}$ (as \ast$\ast$-rings).