We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X be a compact metric space and let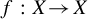 
$f: X\!\rightarrow \! X$ be a homeomorphism on X. We show that if f is both pointwise recurrent and expansive, then the dynamical system 
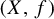$(X, f)$ is topologically conjugate to a subshift of some symbolic system. Moreover, if f is pointwise positively recurrent, then the subshift is semisimple; a counterexample is given to show the necessity of positive recurrence to ensure the semisimplicity.
