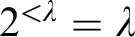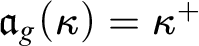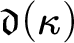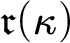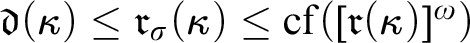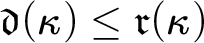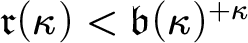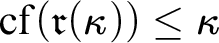2 results
MORE ZFC INEQUALITIES BETWEEN CARDINAL INVARIANTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 897-912
- Print publication:
- September 2021
-
- Article
- Export citation
INFINITE COMBINATORICS PLAIN AND SIMPLE
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1247-1281
- Print publication:
- September 2018
-
- Article
- Export citation