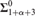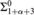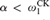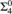2 results
CALIBRATING DETERMINACY STRENGTH IN LEVELS OF THE BOREL HIERARCHY
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 510-548
- Print publication:
- June 2017
-
- Article
- Export citation
DEFINABILITY OF SATISFACTION IN OUTER MODELS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 14 September 2016, pp. 1047-1068
- Print publication:
- September 2016
-
- Article
- Export citation