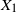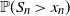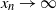2 results
Large-deviation results for triangular arrays of semiexponential random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 399-420
- Print publication:
- June 2022
-
- Article
- Export citation
The variance of a truncated mixed exponential process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 167-179
- Print publication:
- March 1994
-
- Article
- Export citation